Linear integrală și circulația câmpului vectorial

Determinarea liniare integrale

Să presupunem că în domeniul spațial $ \ mathbf> $ este un câmp vectorial continuu $ \ bar (\ mathbf>), \ mathbf> $ - curba neteda situată în $ \ mathbf> $. Integrala linie de câmp $ \ bar $ de-a lungul liniei $ \ mathbf> $ se numește linie integrală pe lungimea arcului de produs interior $ \ bar (\ mathbf>) $ pe vectorul $ \ bara unitate tangent (\ mathbf>): W = \ int \ limits_L (M) \, DS> $.

Deoarece fluxul acestei integrale pot fi prezentate în diferite moduri. Deci, atunci când considerați că produsul de $ \ bar $ (M) în $ DS $ dă schimbarea vectorului raza de punctul $ \ mathbf> $, adică, $ \ Bar \ cdot ds = d \ bar = dx \ bar + dy \ bar + dz \ bar $, atunci $ W = \ int \ limits_L> $ si $ W = \ int \ limits_L $. În consecință, linia integrală, și poate fi exprimată printr-o liniară integrantă a coordonatelor.

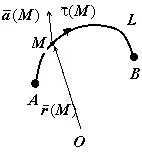
Sensul fizic al integrale liniare.

în cazul în care $ \ bar (\ mathbf>) $ - câmp de forță, de $ W $ este câmpul în acest moment se deplasează materialul de-a lungul unei linii $ \ mathbf> $ vezi integralele triple ..

Proprietățile de bază ale integrant liniare.

$ \ Int \ _ \ limite, DS> = \ int \ _ \ limite, DS> + \ int \ limite _ \, DS> $. Direcție pe fiecare din părțile de $ \ mathbf> _ $ si $ \ mathbf> _ $ trebuie să fie aceeași ca și întreaga curbă $ L_1 \ ceașcă L_2 $,

3). În cazul în care direcția de-a lungul $ \ mathbf> $ liniare modificări integrale semna.

Acest lucru rezultă din faptul că vectorul $ \ bara (\ mathbf>) $ este schimbat la - $ \ bar (\ mathbf>) $.

4). Dacă $ \ mathbf> $ - linie de câmp vectorial și se deplasează în direcția câmpului, apoi $ \ mathbf >> 0 $. În acest caz, vectorul $ \ bara (\ mathbf>) $ coliniar $ \ bar (\ mathbf>) $, deci $ \ bar \ cdot \ bar = \ mathop \ bar> \ limits_> = \ vert \ bar \ vert> 0 $.

Calculul liniei integrale

Ca orice linie integrală, linie integrală este calculată prin reducerea la integrală definită a curbei parametru de linie în mod tipic calculat integral $ W = \ int \ limits_L $. În cazul în care curba cu specificarea prin parametri nu este de forma $ L: \ left \ \ Dreapta. t_0 \ leqslant t \ leqslant t_k $, unde $ x (t), \, y (t), \, z (t) $ - funcția continuu diferențiabilă, atunci $ W = \ int \ limits_L = \\ = \ int \ limitele _ ^ '(t) + Q (x (t), y (t), z (t)) \ cdot' (t) + R (x (t), y (t), z (t)) \ cdot „(t)> \ dreapta] dt>. $

integrând direcția de mișcare determinată de direcția curbei.

câmp vectorial Circulation

Circulația se numește integrala linia câmpului vectorial pe o curbă închisă $ \ mathbf> $: U $ = \ oint \ limits_C> $.

Se spune de obicei că circulația caracterizează capacitatea de rotație a câmpului. Aceasta se referă la următoarele. În cazul în care liniile de câmp vectorial sunt închise, apoi, după cum am văzut, circulația lor în direcția câmpului este pozitiv, în timp ce în interpretarea hidrodinamică a particulelor de filare lichid la aceste linii închise. Să presupunem acum că liniile de curent sunt arbitrare, imaginați-vă în valoare de $ \ mathbf> $ un contur închis $ \ mathbf> $. În cazul în care, ca urmare a mișcării fluidului, acest circuit se va roti câmpul are o capacitate de rotație, valoarea absolută a circulației va determina viteza unghiulară U $ \ vert $, cea mai mare viteza>, marca de circulație se va indica dacă direcția de rotație coincide cu direcția integrării.

A se vedea, de asemenea:

aplicarea mecanică a dublei integralei

Calculul integralei de suprafață a primului tip

Proprietățile integralelor duble

Formula. Funcții de egalitate și formule de echivalență. echivalență cheie

Du-te la conținut $ \ rightarrow \ rightarrow \ rightarrow $