Legătura dintre graficul funcției și graficul derivatului său - soluționarea problemelor de control

Legătura dintre graficul funcției și graficul derivatului său

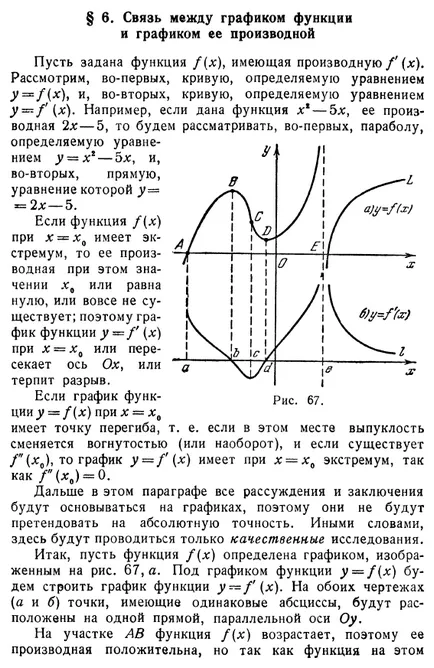
Legătura dintre graficul funcției și graficul derivatului său Fie o funcție f (x)> având un derivat / „(x). Luați în considerare, în primul rând, curba definită de ecuația y

/ (X), și, în al doilea rând, curba definită prin ecuația y = zf (x). De exemplu, dacă o anumită funcție x * - 5ls, derivatul său 2-5, atunci vom considera, în primul rând, parabola este definită de ecuația y - x - oh, și, în al doilea rând, o linie dreaptă, a cărei ecuație este y = == 2 - 5. Dacă funcția / (x) la x = x0 are un extremum, derivatul său la această valoare x0 sau egală cu zero, sau nu există; prin urmare, graficul y - f (x) x = x0 sau axa x cruci sau discontinuitate. Dacă graficul din figura funcției g7 TION y = f (x) x = x0 este un punct de inflexiune, adică, în cazul în care, în acest moment înlocuit convexitate concavitate (sau invers) și există f „(x0), apoi graficul y .. - f '

4) '8 (* + 2)' 3 3 și în § 3, capitolul III a fost construit hsh- parabolei y ^ = arg; leg- luna martie 3 pentru a vedea că funcția x-CH este un derivat al (x-1x4-2) funcția v-V>. Dacă vom combina aceste funcții grafice ale tions, vom obține imaginea prezentată în Fig. 68. Această cifră confirmă cele de mai sus. Exerciții la capitolul. VIII 1. Găsiți valorile critice și de a explora pe scăderea și creșterea funcției y = -16 xm x. 2. Găsiți valorile critice și de a explora în creștere și scăderea funcției # = X9 + ^ -X * + U 3. Găsiți valorile critice ale funcției y - f *. 4. Găsiți valorile critice ale funcției