Integralele linie de primul tip

Să presupunem că curba \ (C \) este descrisă de o funcție vector \ (\ mathbf = \ mathbf \ stânga (s \ dreapta), \) \ (0 \ le s \ le S \) în cazul în care variabila \ (s \) reprezintă lungimea arcului curba (Figura \ (1 \)).

Dacă curba \ (C \) este determinată funcției scalare \ (F, \), atunci \ integral (\ int \ limits_0 ^ S \ left (s \ dreapta)> \ dreapta) ds> \) este numit integrantă linie de primul tip de funcții scalare \ (F \) de-a lungul curbei \ (C \) și este desemnat ca \ [\ int \ limits_C \ dreapta) ds> \; \; \; \ textul \; \ ;. \ int \ limits_C \] linia \ integral (\ int \ limits_C \) există, în cazul în care funcția \ (F \) este continuă pe curba \ (C \)

Proprietățile unei linii integrantă a primului tip

De \ integrantă linie (I \) un fel are următoarele proprietăți:

Integral nu depinde de orientarea curbei;

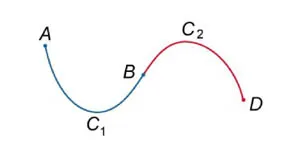
Să presupunem că curba \ (\) începe de la un punct \ (A \) și se termină la punctul \ (B \) și curba \ (\) începe de la un punct \ (B \) și se termină la punctul \ (D \) (Figura \ (2 \)). Apoi, combinarea lor se va numi curba \ (\ cupa, \) care se extinde de la \ (A \) la \ (B \) de-a lungul curbei \ (\) și apoi de la \ (B \) la \ (D \) de-a lungul curbei \ Pentru integralelor curbilinii de primul tip de relație \ (\.) [\ int \ limits_ \ cup> = \ int \ limits_> + \ int \ limits_>; \]

Găsiți integral \ (\ int \ limits_C yds> \) de-a lungul segmentului liniei \ (y = x \) de la origine la punctul \ (\ stânga (\ dreapta) \) (Figura \ (3 \)).

Calculați \ integral (\ int \ limits_C ds> \) unde \ (C \) - arc \ (x = o \ cos t, \) \ (y = a t \ păcat \) \ (0 \ le t \ le \ mare \ frac \ normalsize. \)

Calculați \ integral (\ int \ limits_C ds> \) unde \ (C \) - curba definită de ecuația \ (y = f \ stânga (x \ dreapta) = \ ln x, \) \ (1 \ le x \ Le e. \)

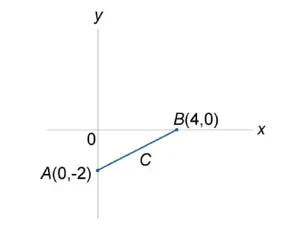
Se calculează integralei \ (\ int \ limits_C, \) unde \ (C \) este segmentul de linie din punct \ (O \ stânga (\ dreapta) \) la \ (A \ stânga (\ dreapta) \) (Figura \ (4 \) de mai sus).

Calculați \ integral (\ int \ limits_C +> \ dreapta) ZDS>, \), în cazul în care curba \ (C \) este definit parametrically ca \ (\ mathbf \ stânga (t \ dreapta) = \ stânga (\ dreapta), \) \ (0 \ le t \ le \ pi. \)

Calculați linia \ integral (\ int \ limits_C >> \ normalsize> \), în cazul în care curba \ (C \) - un segment de linie din punctul \ (\ stânga (\ dreapta) \) la \ (\ stânga (\ dreapta) \) (Figura \ (5 \)).