Filtre digitale Recursive și non-recursive - studopediya

Unitatea de control digital poate efectua dispozitivul funcția de corectare în bucla de control. hardware sau software punerea sa în aplicare există un filtru digital. În general, filtrul discret PF are forma

în care unii dintre coeficienții poate fi zero. Dacă împărțim numărătorul și numitorul de zn. obținem

.

Notând de intrare și de ieșire semnale ale filtrului, respectiv e și u, și având în vedere că. obținem ecuația

Având în vedere faptul că semnalele de întârziere medii u și e în intervale discrete k. trecerea la ecuația inițială și rezolvarea în raport cu valoarea curentă a semnalului de comandă uk. obține

Astfel, pentru determinarea semnalului de comandă pe intervalul k necesar să aibă valorile valorilor de intrare și de ieșire ale filtrului pe intervalele n precedente, unde n - ordinul PF filtru.

Dacă = a1. AN = 0, se numește un filtru non-recursivă. Acesta utilizează informații despre valorile anterioare doar la intrare.

Filtrul digital este numit recursiv. în cazul în care utilizează informații cu privire la valorile de la ieșirea din intervalele precedente.

Structura unui PF filtru recursiv (2.12) pentru n = 2 se obține, dacă introducem variabile auxiliare

Apoi U0 variabila (z) pe baza expresiei (2.13), obținem

.

Această expresie este realizată structura prezentată în Fig. 2.12 două unități de întârziere în legătura directă și feedback negativ a1 / a2 și a0 / a2. Valoarea filtrului de ieșire este obținută pe baza expresiei

realizat structural prin însumare la nivelul de ieșire (vezi. fig. 2.12). Rezultat Diagrama bloc poate servi ca bază pentru implementare hardware. În care fiecare element de întârziere simbolizează memoria de stocare variabilă pe parcursul unui interval de discretă, iar fiecare legătură înseamnă multiplicarea variabilă inertialess cu un factor constant. însumarea nod implementat totalizator.

Implementarea software se bazează pe calcularea uk algoritm conform formulei (2.13).

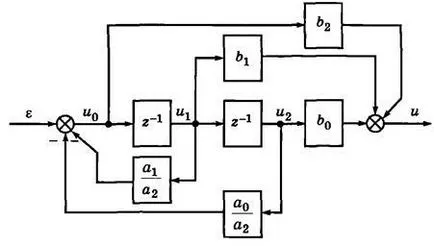
Fig. 2.12. Structura unui filtru digital recursiv

1. Besekersky VA Popov EP Teoria sistemelor automate de control - M. Nauka, 1972. - 768 p.

4. Voronov AA Bazele teoriei de control automat, controlul automat al sistemelor liniare continue. - M. Energie, 1980. - 312 p.

6. Popov EP Teoria sistemelor liniare de control și management automat. - M. Nauka, 1989. - 304 p.

7. Solodovnikov VV Plotnikov VN AV Yakovlev Teoria de bază și elemente de sisteme de control automat. - M. Inginerie Mecanică, 1985 - 536

8. EI Yurevich Teoria de control automat. - L. Energie, 1975. - 416 p.

[1] din latinescul "recurrere" - "înapoi"