Elipsă și ecuația canonică

Definiția 3.5.2. Elipsă este mulțimea tuturor punctelor în plan, suma
distanțele de la care la cele două puncte de date de pe acest plan, numite focare, acolo
o valoare constantă egală cu 2a.
Ecuația canonică a elipsei este dată de

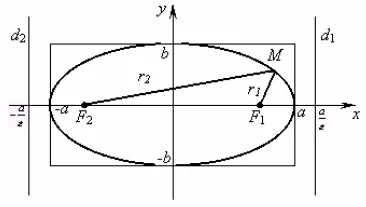
unde a - semiaxa mare; b - axa minoră. Punctele F1 (c, 0) și F2 (-c, 0) - c numit
focarele elipsei, forma elipsă (o masura a compresiei acesteia) se caracterizează prin ei
excentricitate
Definiția 3.5.3. raza focală este distanța de la curba la un punct de focalizare.
Focal elipsă raze r1 și r2 sunt legate de
Cu elipsa este asociat cu două linii mari numite directrices d1 sale și
d2. ale căror ecuații sunt de forma. Raportul dintre distanțele din orice punct al elipsei
să se concentreze la distanța corespunzătoare excentricitatea elipsei este egal cu directricea # 949;.

Un caz special al ecuației elipsei când ecuația este un cerc centrat la punctul O (0,0) și raza a. Ecuația canonică a unui cerc cu
centru de la punctul O „(a, b) și raza r este dat.
Alte ecuații canonice ale curbelor eliptice:
Ecuația 1 specifică punctul O (0,0);
Ecuația 2 specifică o elipsă imaginară;
3. Ecuația definește cercul imaginar.