Elemente de geometrie diferențială este o parametrizare naturală - rezolvarea problemelor, controlul

Elemente de geometrie diferențială parametrizare naturală

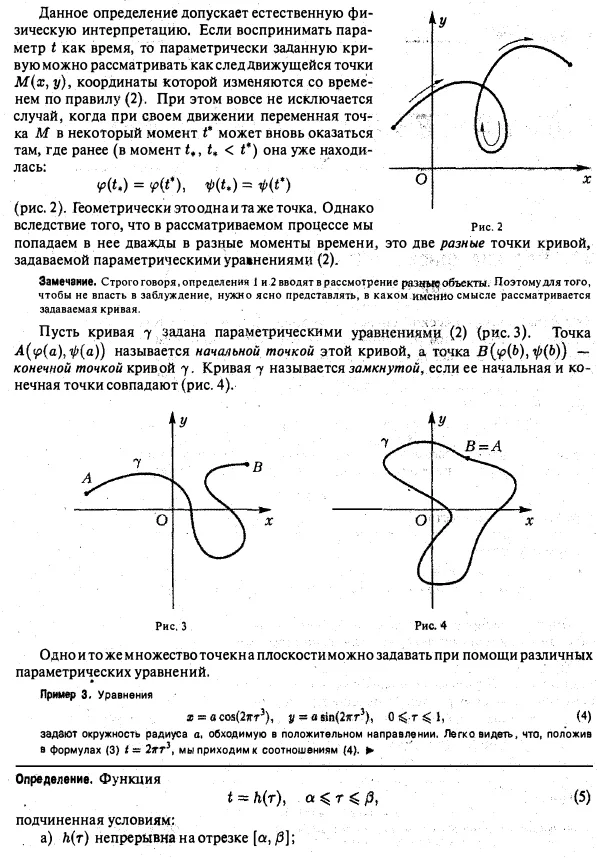
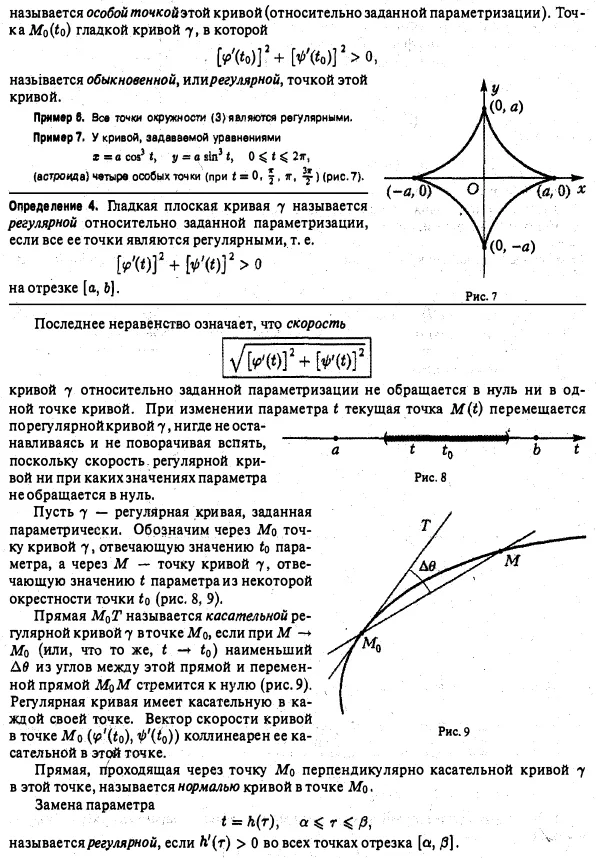
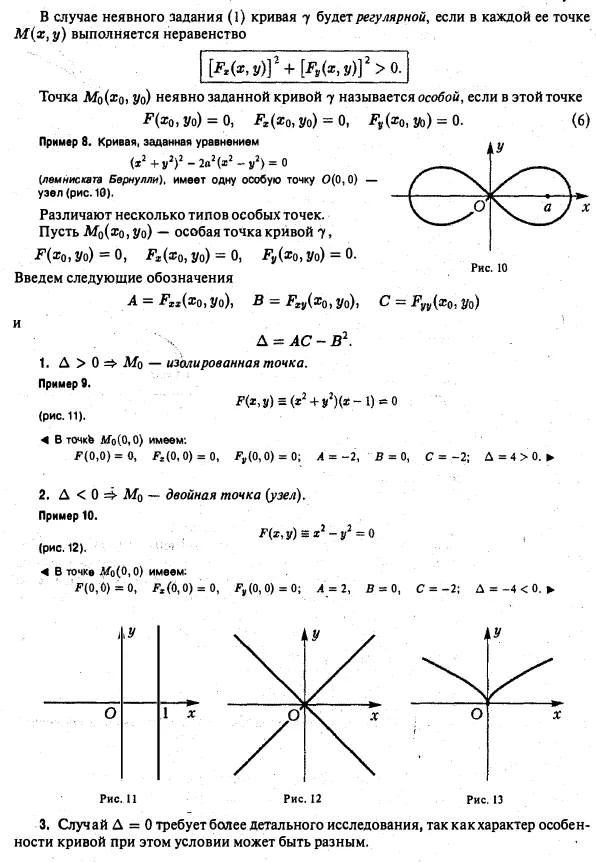
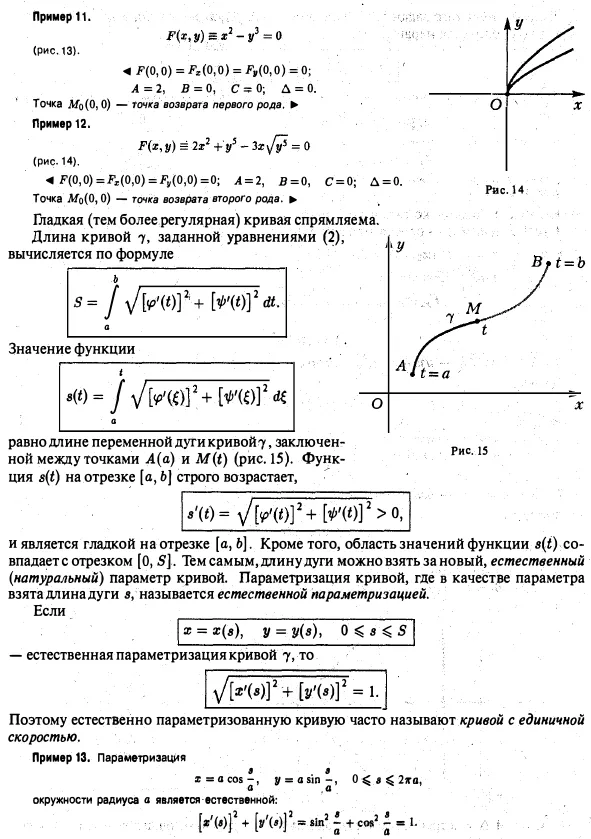
Ilustrativ geometric mânca prea - curba planar - definiția aerului de aprovizionare duce la mai multe diferite, deși concepte similare. Curba plan poate fi înțeleasă ca un set de puncte într-un plan și planul setului de puncte cu secvența de transmitere a acestora - orientarea. Noi oferim două abordări cele mai comune pentru a determina care este o curbă plană. Lăsați planul administrat cartezian rectangular sistem de coordonate Oxy. Definiție 1 (metoda de referință implicită). Curba plan este multimea punctelor M 7 coordonate plane x și y, care atunci când sunt substituite în ELEMENTS ecuație geometria diferențială a curbelor plane. Metode de sarcina. parametrizare naturală transformându-l într-o identitate. Exemplul 1. Ecuația. definește un cerc de rază centrată la 0 (0,0) 3]; c) valorile regiune ale funcției h (r) - intervalul [a, b] se numește curbă continuă parametru de înlocuire 7 (Figura 5) .. Elemente de geometrie diferențială a curbelor plane. Metode de sarcina. Înlocuirea parametrizare naturale în formulele (2) parametrul t prin funcția A (t), obținem ecuația - o altă parametrizare 7. Orice curbă poate fi curba parametrizat în mai multe moduri diferite. Definiție 3. O curbă plană 7 se numește n-relativ buna dacă funcția parameterization) aparține. În cazul în care funcțiile neimportante ordinul n netezime, atunci vorbim de o curbă lină. Exemplul 4. Curba este dată de ecuațiile 3 netede (Fig. Sub a). Exemplul 7 S. Curba definită prin ecuațiile 2 este netedă. Cu toate acestea, seturile de puncte în planul descris de aceste ecuații, • are un punct O (dacă t) caracteristica - îndoitură (ris.vb). Acest lucru înseamnă că netezimea funcțiilor. definind o curbă, aceasta nu oferă o schimbare lină. Rețineți că derivații acestor funcții în todnovremenno tratate ca zero. Tchka Mo curba lină la t0 valoarea parametrului corespunzător, M0 care este numit un punct singular al curbei (în raport cu o parametrizare predeterminată). Mo punct (xo) curba neteda 7, care este denumit comun, nshregulyarnoy, punctul acestei curbe. Exemplu c. Toate punctele de cerc (3) sunt regulate. Exemplul 7. Curba definită prin ecuațiile (astroidă) patru punct singular (la t w 0, | ultima inegalitate înseamnă că curba 7 parametrizarea viteză predeterminată relativă nu devine zero, în orice punct al curbei Când parametrul t punctul curent M (. t) se deplasează curba poregulyarnoy 7, navlivayas nicăieri reziduale și fără să se întoarcă înapoi, deoarece viteza de curbe regulate pentru orice valoare a parametrului nu dispare Să 7 - .. o curbă regulată definită parametric denota Mo 7 curba punctul znach corespunzătoare INJ £ a parametrului, și prin M -. Punctul curba 7 corespunde valorii t parametru dintr-un cartier de puncte (. Figura 8, 9) Direct M0T numit tangentă curbă regulată 7 Mo vtochke, în cazul în care (sau, echivalent,) A0 cea mai mică dintre unghiurile dintre această linie dreaptă și MQM variabilă tinde la zero (vezi Fig. 9). curba normală are o tangentă la fiecare punct. curba vitezei vectorului la punctul de coliniare sale Mo tangentei la acest punct. o linie care trece prin punctul Mo 7 perpendicular pe tangenta curbei la acest punct se numește curba normală vtoch e Mo. parametru de substituție numit regulat y dacă este N (t la toate punctele intervalului [a, / 3]. În cazul implicit referire (1), curba 7 va fi regulat dacă la fiecare punct M (x, y) satisface inegalitatea punct Mo (xo > Vq) dat implicit curba 7 se numește singular dacă, în acest moment exemplul 8. curba definită prin ecuația (lemmisyuga Bernult) are un punct singular 0 (0,0) -. Ansamblu (Figura 10) Există mai multe tipuri de puncte singulare. Să M0 (xo, yo) - punctul singular 7, se introduce următoarea notație returnează primul exemplu tip 12 (fig. 14) - .. cuspid doilea tip Ch. dkaya (mai ales regulate) Curba care se poate rectifica. Lungimea curbei 7, dată de ecuațiile (2), se calculează valoarea formulei a funcției egală cu lungimea krivoy7 arc variabil cuprins între punctele (Fig. 15). Funcția în intervalul [a, 6) strict în creștere, Exemplul 11. ELEMENTELE geometria diferențială a curbelor plane. Metode de sarcina. parametrizare naturală și este netedă în intervalul [a, 6]. În plus, valoarea funcției zonă s (t) coincide cu intervalul [0, 5]. Astfel, lungimea arcului poate fi luată ca un cadru nou, natural (natural) al curbei. Parametrizare a curbei, în care parametrul este preluat din lungimea arcului, se numește parametrizare naturală. Dacă parametrizare naturală a curbei, prin urmare, este curba parametrizată naturală este adesea menționată ca o curbă cu o singură rată. Exemplul 13. Parametrizarea raza cercului este naturală: