ecuații exponențiale și inegalități

decizie Majoritatea problemelor matematice într-un fel sau altul legătură cu conversia numerică, algebrice sau expresii funcționale. Cele de mai sus se aplică în special la decizia de ecuații exponențiale și a inegalităților. În exemplele de realizare USE probleme de matematica pentru acest tip includ, în special, C3 sarcină. Aflați cum să rezolve sarcina C3 este importantă nu numai pentru a trece cu succes examenul, dar, de asemenea, pentru motivul că această abilitate este utilă în studiul matematicii în liceu.

Înainte de a proceda la o analiză ecuații exponențiale specifice și inegalități. ca tutore în matematică, vă sugerez să perie pe unele materiale teoretice de care avem nevoie.

funcție exponențială

Ce este o funcție exponențială?

Funcția de forma y = a x. unde a> 0 și un ≠ 1, se numește funcția exponențială.

Proprietățile principale ale funktsiiy exponențială = a x:

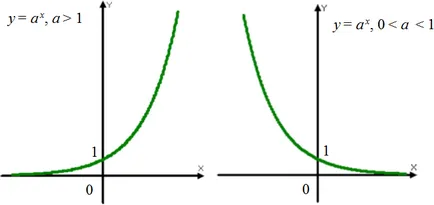
Graficele de funcții exponențiale (exponențială)

Soluție de ecuații exponențială

Ilustrative sunt ecuații în care variabila necunoscută este doar în ceea ce privește orice grad.

Pentru a rezolva ecuațiile exponențiale trebuie să știe și să fie capabil de a utiliza următoarea teoremă simplu:

În plus, este util să ne amintim despre formulele de bază și acțiunile cu grade:

Exemplul 1. Rezolvați ecuația:

Soluție: Folosind formula de mai sus și substituția:

Ecuația devine atunci:

Discriminantul ecuației pătratice obținut este pozitiv:

Aceasta înseamnă că ecuația are două rădăcini. Găsiți-le:

Revenind pentru a inversa schimbarea, obținem:

A doua ecuație nu are rădăcini, deoarece funcția exponențială este strict pozitivă pe întregul domeniu. Rezolva al doilea:

Acestea fiind spuse, Teorema 1 trece la o ecuație echivalentă: x = 3. Aceasta ar fi un răspuns la locul de muncă.

Exemplul 2: rezolva ecuația:

Soluție: restricții privind intervalul de valori admisibile pentru ecuația au, ca expresie radicală are sens pentru orice valoare a lui x (funcția exponențială y = X9 aprilie, este pozitiv și nu este zero).

Rezolvarea ecuației prin utilizarea echivalente regulilor de transformare înmulțire și împărțire grade:

Ultima tranziție a fost realizată în conformitate cu Teorema 1.

Exemplul 3: rezolva ecuația:

Soluție: ambele părți ale ecuației inițiale poate fi împărțită la 0,2 x. Această tranziție ar însemna, deoarece această expresie este mai mare decât zero pentru orice valoare a lui x (funcția exponențială este strict pozitivă pe domeniul său). Apoi, ecuația devine:

Exemplul 4. Rezolvați ecuația:

Solutia: simplifica ecuația elementar prin conversii echivalente folosind redusă de la început, regulile de divizare și multiplicare de grade:

Impartind ambele părți ale ecuației de 4 x. Ca și în exemplul anterior, este echivalent cu transformare, deoarece expresia nu este egal cu zero pentru orice valoare a lui x.

Exemplul 5 Rezolva ecuația:

Soluție: Funcția y = 3 x. partea stângă a ecuației, este în creștere. Funcția y = -x -2/3, partea dreaptă a ecuației este în scădere. Acest lucru înseamnă că, dacă graficele acestor funcții se suprapun, atunci nu mai mult de un punct. În acest caz, nu este greu de ghicit că graficele se intersectează în punctul x = -1. Alte rădăcini nu.

Exemplul 6. Rezolvați ecuația:

Solutia: simplifica ecuația de conversii echivalente, ținând cont întotdeauna că funcția exponențială este strict mai mare decât zero pentru toate valorile lui x și utilizând regulile de calcul al produsului și coeficientul de grade acordate la începutul articolului:

demonstrație Soluție inegalităților

Exemple ilustrative numit inegalitate, în care variabila necunoscută este conținută numai în executarea oricăror puteri.

Pentru a rezolva inegalitățile exponențiale necesită cunoașterea următoarea teoremă:

Exemplul 7. Solve inegalitate:

Soluție: Să presupunem inegalitatea inițială în forma:

Se împarte ambele părți ale acestei inegalități de 3 2x. în același timp (din cauza pozitivitatea functia y = 3 2x) semnul inegalității nu se va schimba:

Apoi, inegalitatea devine:

Astfel, soluția a diferenței inegalității este:

trecerea a inversa schimbarea, obținem:

Inegalitatea stânga datorită pozitivitatea funcției exponențiale se realizează automat. Folosind proprietățile cunoscute ale logaritmului, trecem la inegalitatea echivalentă:

Deoarece baza gradului este un număr mai mare de un echivalent (Teorema 2) se va deplasa la următoarea inegalitate:

Deci, vom obține în cele din urmă răspunsul:

Exemplul 8. Solve inegalitate:

Soluție: Folosind proprietățile de înmulțire și împărțire a puterilor, rescriem inegalitatea ca:

Vom introduce o nouă variabilă:

Având în vedere această inegalitate de substituție devine:

Înmulțim numărătorul și numitorul de 7, obținem următoarea inegalitate echivalentă:

Deci, inegalitatea satisfac următoarele valori ale variabilei t:

Apoi, întorcându-se pentru a inversa schimbarea, obținem:

Deoarece baza puterii este mai mare decât unu, este echivalent cu (teorema 2) se vor deplasa la inegalitatea:

În cele din urmă vom obține răspunsul:

Exemplul 9. Solve inegalitate:

Se împarte ambele părți ale inegalității în expresia:

Este întotdeauna mai mare decât zero (din cauza pozitivitatea funcției exponențiale), astfel încât nu este nevoie să se schimbe semnul inegalității. obținem:

Noi folosim schimbarea de variabile:

Ecuația originală devine atunci:

Deci, inegalitatea satisface valori ale lui t. situat în diferența:

Revenind la spate schimbarea constatăm că inegalitatea inițială este împărțit în două cazuri:

Prima soluție a inegalității nu se datorează pozitivitatea funcției exponențiale. Rezolva al doilea:

Deoarece baza puterii în acest caz a fost mai mică decât una, dar mai mare decât zero, echivalent cu (Teorema 2) se va deplasa la următoarea inegalitate:

Deci, răspunsul final:

Exemplul 10. Decide inegalitatea:

Ramurile parabolei y = 2x + 2x 2 îndreptat în jos, prin urmare, este limitată mai sus de valoarea pe care acesta ajunge la vertexului:

Ramurile parabolei y = x 2 -2x +2, stând în exponentul sunt îndreptate în sus, astfel încât acesta este limitat la o valoare sub care se ajunge la vertexului:

Împreună cu aceasta este mărginită de mai jos si functia y = 3 x 2 -2x +2. pe partea dreaptă a ecuației. Aceasta a atins cea mai scăzută valoare în același punct ca parabole în picioare în index, iar valoarea este de 3 1 = 3. Astfel, inegalitatea inițială poate fi adevărat numai în cazul în care funcția este o funcție de stânga și dreapta sunt luați la aceeași valoare litera egal cu 3 (intersecția intervalelor acestor funcții este doar un număr). Această condiție este îndeplinită la un singur punct x = 1.

Pentru a învăța să rezolve ecuații exponențiale și inegalități, trebuie să antreneze în mod constant în decizia lor. În această chestiune dificilă vă poate ajuta la o varietate de manuale, culegeri de probleme de matematică elementare, colecții de sarcini competitive, cursuri în matematică la școală, precum și sesiuni individuale cu un antrenor profesionist. Eu sincer vă doresc succes în pregătirea și rezultate excelente la examen.