ecuație liniară și exemplele cu formula

Vedere generală a unei ecuații liniare, cu o singură necunoscută, iar principiul soluțiilor sale

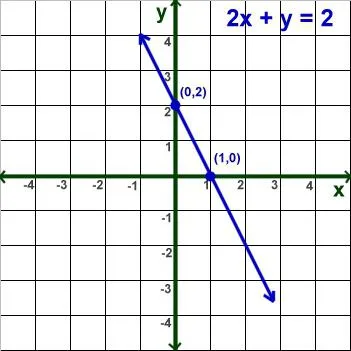
Orice ecuație care poate duce la un astfel de tip de inregistrare:

Se numește liniar. Aceasta este o formulă comună. Dar, de multe ori în ecuațiile liniare quest scrise într-o formă implicită. Atunci când doriți să efectuați transformări identice pentru a obține înregistrarea convențională. Aceste acțiuni includ:

Divulgarea între paranteze;
mutați toți termenii cu variabila din partea stângă, iar restul - la dreapta;
reducerea termeni similari.

În cazul în care cantitatea necunoscută în numitorul fracției, este necesar să se determine valoarea sa, în care expresia nu are nici un sens. Cu alte cuvinte, se presupune să cunoască domeniul ecuației.

Principiul pe care se rezolvă toate ecuațiile liniare, se reduce la, pentru a partaja valoarea pe partea dreaptă a ecuației prin coeficientul în fața variabilei. Aceasta este, „x“ este egal cu / a.

Cazuri speciale de ecuații liniare și soluțiile lor

In timpul argumentelor pot apărea astfel de momente, când ecuațiile liniare iau una dintre speciile particulare. Fiecare dintre ele are o soluție specifică.

În prima situație:

Soluțiile acestei ecuații va fi întotdeauna x = 0.

În al doilea caz, „o“ are o valoare egală cu zero:

Răspunsul acestei ecuații va fi orice număr. Asta este, el are un număr infinit de rădăcini.

A treia situație este după cum urmează:

Această ecuație nu are nici un sens. Deoarece rădăcinile satisface aceasta, nu există.

Forma generală a ecuațiilor liniare în două variabile

De la numele său, este clar că necunoscutele în ea pentru două. ecuații liniare cu două variabile arata astfel:

Deoarece înregistrarea există două necunoscute, răspunsul va apărea ca o pereche de numere. Acest lucru nu este suficient pentru a specifica doar o singură valoare. Acesta este un răspuns incomplet. O pereche de valori pentru care ecuația devine o identitate, este o soluție. Și întotdeauna a scrie prima variabilă în răspunsul care vine mai devreme în alfabetul. Uneori se spune ca aceste numere să-l satisfacă. Mai mult, astfel de perechi poate fi un număr infinit.

Cum de a rezolva ecuația liniară cu două necunoscute?

Pentru a face acest lucru, pur și simplu ridica orice pereche de numere care ar fi adevărat. Pentru simplificare, puteți lua una dintre necunoscutele este egal cu orice număr prim, și apoi găsi de-al doilea.

Atunci când este adesea necesar să se efectueze acțiuni pentru a simplifica ecuatia deciziei. Ele se numesc transformări identitare. Iar pentru ecuații țineți întotdeauna următoarele proprietăți:

fiecare termen poate fi transferat în partea opusă a ecuației și înlocuiți-l cu semnul opus;
la stânga și dreapta orice ecuație este permis să fie împărțită în același număr în cazul în care nu este zero.

Exemple de sarcini cu ecuații liniare

Prima sarcină. Pentru a rezolva ecuația liniară: 4 = 20, 8 (x - 1) 2 + 2 = (4 - 2); (5x + 15) / (x + 4) = 4; (5x + 15) / (x + 3) = 4.

În ecuația, care este primul în listă, pur și simplu efectua o divizare prin 4. Rezultatul 20 este egal cu 5. Acesta este răspunsul x = 5.

A treia ecuație impune ca transformarea identității a fost finalizată. Acesta va fi în divulgarea parantezele și colectarea alți termeni asemănători. După prima acțiune a ecuației devine: 8x - 8 + 2 = 8-4. Apoi, aveți nevoie pentru a muta toate necunoscutele din partea stângă, iar restul - spre dreapta. Ecuația va arata astfel: 8x + 2x + 4 = 8 + 8 După aducerea acestor termeni: 14x = 16. Acum, se pare la fel ca și prima, iar decizia sa este ușor. Răspunsul este x = 8/7. Dar matematica se presupune a aloca porțiunea întreagă a fracțiunii necorespunzătoare. Apoi, rezultatul va fi transformat, iar „x“ este egal cu un întreg și a șaptea.

În alte exemple, variabilele sunt la numitor. Acest lucru înseamnă că trebuie mai întâi să afle pentru ce sunt definite valori ale ecuației. Pentru a face acest lucru, aveți nevoie pentru a elimina numărul în care numitorii dispar. În primul exemplu este „-4“, a doua este „-3“. Asta este, aceste valori ar trebui să fie excluse din răspunsul. După aceea trebuie să multiplice ambele părți prin expresia în numitor.

Scoaterea suporturilor și aducerea acestor termeni, în prima dintre aceste ecuații se obține: 5x + 4 + 15 = 16, iar cea de a doua 5x + 15 + 4 = 12. Deoarece prima ecuație pentru această transformare este x = -1. Al doilea este egal cu „-3“, ceea ce înseamnă că deciziile finale nu este.

Cea de a doua sarcină. Pentru a rezolva ecuația: 7h + 2y = 5.

Să presupunem că primul necunoscut x = 1, atunci ecuația devine -7 * 1 + 2y = 5. Prin deplasarea spre partea dreapta a factorului „-7“ și schimbându-l la un semn plus, veți obține că 2y = 12. Asta înseamnă că = 6. Răspuns: Una dintre soluțiile ecuației x = 1, y = 6.

Forma generală a inegalității cu o singură variabilă

Toate situațiile posibile pentru inegalitățile sunt prezentate aici:

În general, se pare ca o ecuație liniară simplă, doar semnul de egalitate se înlocuiește cu inegalitatea.

Condiții de transformări identitare ale inegalității

Precum și ecuații liniare și inegalități pot fi modificate în funcție de anumite legi. Acestea sunt după cum urmează:

în partea stângă și dreaptă, puteți adăuga orice expresie alfabetice sau numerice, semnul inegalității va rămâne aceeași;
pot fi, de asemenea, multiplicate sau împărțit același număr pozitiv din acest semn nu este schimbat din nou;
înmulțit sau împărțit același număr negativ rămâne adevărată egalitate cu condiția schimba semnul inegalității este inversat.

Vedere generală a dublei inegalitatea

pot fi prezentate probleme, întruchipările inegalități:

Dublează este numit, deoarece semne limitate de inegalitate pe ambele părți. Acesta este rezolvată prin aceleași reguli ca inegalitatea regulate. Și găsirea răspunsul se reduce la o serie de transformări identitare. Până la un simplu.

Caracteristici Soluție dublă inegalitate

Primul dintre acestea este imaginea pe axa de coordonate. Utilizați această metodă pentru inegalități simple, nu este necesară. Dar, în cazuri severe, poate fi doar necesar.

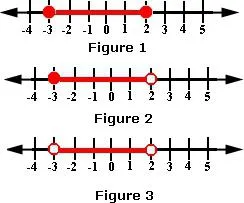
Pentru imagini de inegalitate trebuie notat pe axa tuturor punctelor, care sunt obținute în timpul discuțiilor. Aceste valori invalide, care sunt indicate prin puncții și valorile inegalității, obținem după transformare. Aici, de asemenea, este important să se elaboreze un punct. În cazul în care inegalitatea strictă, adică, <или>, aceste valori sunt înțepat. În inegalitățile non-stricte în ceea ce au nevoie pentru a picta.

Apoi, ar trebui să identifice sensul inegalităților. Acest lucru se poate face prin intermediul unei trape sau arce. intersecția lor va indica răspunsul.

A doua caracteristică este legată de contul său. Acesta oferă două opțiuni. În primul rând - aceasta este inegalitatea finală. Al doilea - în formă de timp. Aici, cu este că există dificultăți. intervale de răspuns întotdeauna arată ca o variabilă cu semnul de accesorii si paranteze cu numere. Uneori devine un interval de biți, în timp ce între paranteze aveți nevoie pentru a scrie caracterul „i“. Aceste semne sunt după cum urmează: ∈ și ∩. lacune între paranteze, de asemenea, joaca un rol. Runda a pus atunci când punctul este exclus din răspunsul, și include o valoare dreptunghiulară. semn al infinitului este întotdeauna în paranteză.

Exemple de soluții ale inegalităților

1. Rezolva inegalitatea 7 - ≥ 5x 37.

După transformări simple, obținute: -5H ≥ 30. Dividing prin "-5" se poate obține o expresie: x ≤ -6. Acesta este răspunsul, dar poate fi scris într-un mod diferit: x ∈ (-∞; -6].

2. Rezolvati dublei Inegalitatea -4 <2x + 6 ≤ 8.

Mai întâi trebuie să scădeți întotdeauna 6. primi: -10 <2x ≤ 2. Теперь нужно разделить на 2. Неравенство примет вид: -5