Divergența câmpului vectorial - studopediya

De interes special este cazul în care debitul calculat prin suprafața închisă. De obicei, în astfel de cazuri, pentru partea pozitivă a suprafeței care primește suprafața exterioară a acestuia. Integrala de suprafață, în acest caz, este indicată după cum urmează:

Când câmpul vectorial este un domeniu al vitezei fluidului. P flux dă diferența dintre cantitatea de lichid care curge din regiunea interioară delimitată de suprafața S. și cantitatea care curge în această zonă. Dacă P = 0, atunci interiorul lichidului curge în același număr ca și există fluxuri. Dacă P> 0, rezultă mai mult fluxuri. Acest lucru înseamnă că există surse din cadrul regiunii. alimentarea unui flux de lichid. În cazul unui câmp electric, acest lucru înseamnă că sarcinile electrice sunt situate în interiorul regiunii. Dacă P <0, это указывает на наличие стоков – мест, где жидкость удаляется из области.

Cea mai importantă caracteristică a surselor și a rezervoarelor este divergenta. Să considerăm un punct M al câmpului vectorial și surround pe suprafața închisă S. calcula câmpul vectorial de flux prin suprafața S închisă și ia acest flux de regiune V raportul de volum delimitat de suprafața S:

Ne găsim acum limita acestui raport, cu condiția ca o regiune delimitată de suprafața S. se micșorează până la un punct M, și anume când V ®0. Această limită se numește vectorul de divergență punctul polyaav M:

Este clar că, dacă există limita, aceasta nu depinde de forma suprafeței S.

Divergenta caracterizează sursa de alimentare sau scurgere. De exemplu, în cazul în care fiecare punct în divergență domeniul vitezei fluidului este zero, înseamnă nu numai o lipsă de surse și chiuvete, dar, de asemenea, că lichidul nu se contracta sau pentru a extinde. Această proprietate, în special, are aer la viteze care nu depășesc aproximativ jumătate din viteza sunetului. Cu toate acestea, la viteze apropiate sau mai mare decât viteza sunetului, aerul se comportă ca un gaz compresibil. Apoi, divergența astfel un gaz nu mai este zero. În mod similar, divergența este nenul dacă acest gaz are reacții chimice (de exemplu, de ardere), schimbarea densitatea. În cazul câmpurilor gravitaționale sau electrice este proporțională cu divergența densității masei sau sarcină, respectiv.

Acum obținem o formulă pentru divergența în sistemul de coordonate carteziene. Lăsați suprafața S are forma unui paralelipiped dreptunghic cu laturile Dx. Dy. Dz. paralele cu axele de coordonate (vezi. Figura 6.6). Scriem integrala de suprafață în determinarea divergenta sumei de trei integralelor duble:

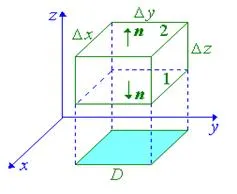
Luați în considerare un al treilea termen:

Fațetele 1 și 2 sunt proiectate în aceeași zonă D pe planul xOy (fețele laterale pot fi ignorate, deoarece acestea sunt perpendiculare pe planul xOy), dar normalele exterioare lor sunt îndreptate în direcții opuse. Presupunând că fețele ecuației z = z1 și z =. Z2 obținem

Bazat pe sensul geometric al unei integrale duble (acesta este volumul situat între planul de coordonate și suprafața descrisă de integrantul):

In mod analog se poate obține formula pentru primul și al doilea termen în expresia

Astfel, am demonstrat următoarea teoremă:

Acest lucru înseamnă că, dacă tot lichidul are aceeași viteză (adică, lichidul se deplasează translationally ca solid), atunci un astfel de debit poate fi nici surse, nici chiuvete.

2) Să presupunem că corpul solid se rotește la o greutate constantă de viteză unghiulară. După cum știm din mecanica teoretică viteza lineară este v = w'r. unde r - vectorul raza unui punct în raport cu punctul de pivotare. Dacă punctul fix luat ca origine, și este orientată de-a lungul axei de rotație a axei Oz, obținem w = sapt. r = xi + yj + zk. atunci

Acest câmp este o viteză liniară de rotație a solidului. Calculăm divergența acest domeniu:

Aceasta înseamnă că trebuie să ne imaginăm un lichid rotativ ca un corp rigid, că într-un astfel de debit poate fi nici canalizare sau surse.

Exemplul 6.4. Găsiți divergența gradientul unui câmp u scalar = x 3 y 2 z la punctul M (1, 1, 1).

Decizie. Am găsit gradientul câmp

și apoi divergența:

Substituind obține coordonatele punctului M.