difracție Fraunhofer printr-o rețea de difracție
Difracția grilaj este un sistem format din fante paralele între shirinya egale dispuse la egal rasstoyaniibdrug altele.
Distanța dintre centrele fante adiacente se numește perioada (constanta) și rețelei de difracție este notată cu d.
În cazul în care lățimea fantei transparente -


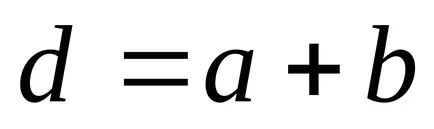
Bună difracție este o placă de sticlă sau de metal, la care dispozitivul de tăiere cu diamant (prin intermediul unor mașini speciale de separare) depuse foarte mult (uneori până la sute de mii) de linii paralele, dispuse la distanțe egale strict una față de cealaltă.
Luați în considerare picătură plan monocromatică val de lumină având o lungime de undă


La fiecare punct B de pe ecran (în planul focal al lentilei) se vor întâlni acele raze care sunt paralele cu lentilele între ele și distribuite la un anumit unghi φ față de direcția undei incidente. Prin urmare, iluminarea în tochkeByavlyaetsya rezultat secundar interferenței undelor de înmulțire kakot porțiuni diferite ale unei fantă, astfel încât sloturi OTH diferite.
Condiții de difracție minimă una fantă determină direcțiile în care amplitudinea oscilației rezultat (intensitate) produsă de fiecare dintre fantele separat, zero (nici unul dintre fantelor nu fascicul direct). Prin urmare, o condiție minimă pentru decalaj audio de difracție va fi, de asemenea, o condiție minimă pentru radere:
,
În aceste direcții în care este direcționat lumina cu fantă, se poate observa ca un maxim în cazul valurilor care provin din diferite fante se potențează reciproc (în fază) și minimele dacă acestea slăbesc reciproc (în fază opusă).
In acele zone pentru care undele de diferență de călătorie care provin din puncte echivalente fante adiacente este egală cu un număr întreg de lungimi de undă (chiar și numărul de jumătăți de valuri)
,
acțiunile tuturor sloturilor se consolidează reciproc. Aceste zone corespund vârfurilor majore.
Principalul maxim al unui anumit ordin se pierde, în cazul în care poziția este aceeași cu unele minimum modelul de difracție dintr-o singură fantă.
Și ce fel de model de difracție între principalele maximelor? Luați în considerare, așa cum va varia iluminarea pe ecran la o trecere treptată de la principalul maxim de ordinul zero (m = 0) la maximul principal de ordinul întâi (m = 1). Pentru a găsi amplitudinea oscilațiilor care rezultă prin utilizarea diagramelor vectoriale. Vectori reprezentând oscilațiile din diferite sloturi

Mai întâi definim amplitudinea oscilațiilor rezultată la φ = 0. În acest caz, vectorii reprezentând oscilațiile din sloturi diferite, paralele între ele și prin adăugarea vectorului va

Intensitatea este proporțională cu pătratul amplitudinii vibrațiilor rezultate. În consecință, intensitatea maximă a zero în N 2 ori intensitatea produsă în direcția uneia fantă.
Prin creșterea unghiului φ între oscilațiile fante adiacente apare aceeași defazajul




.
În ce zone minimele suplimentare vor avea loc?
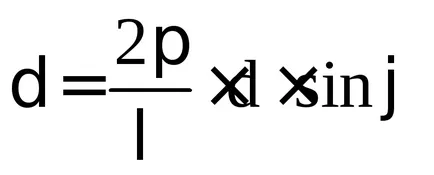

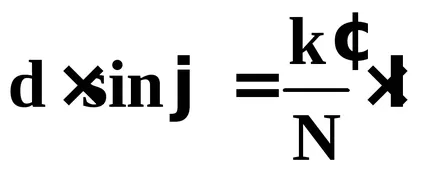
Ce valori pot

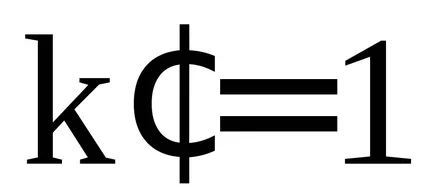
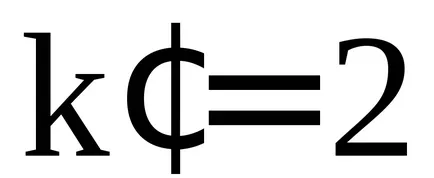
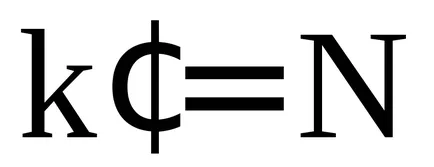
Între oricare două vârfuri principale situate
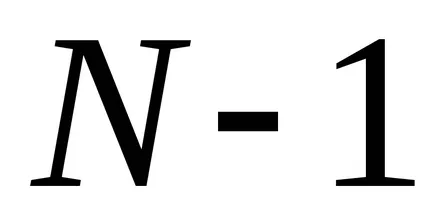

și anume în cazul în care

Este evident că între
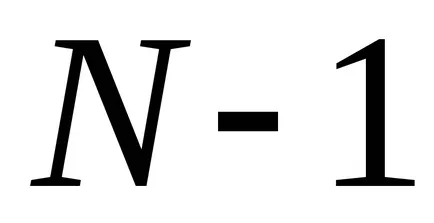
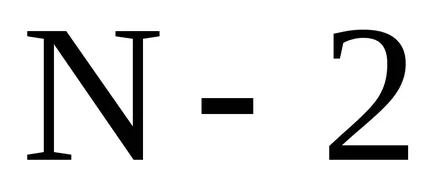

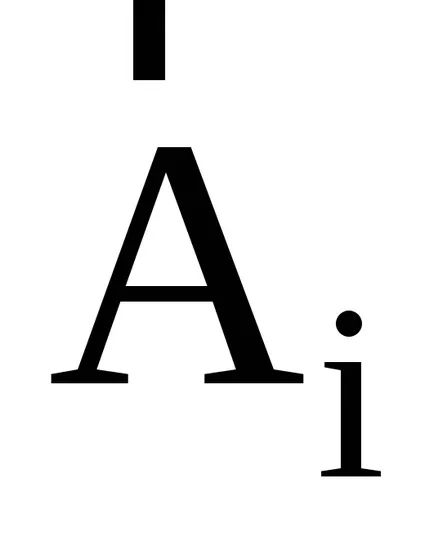
A

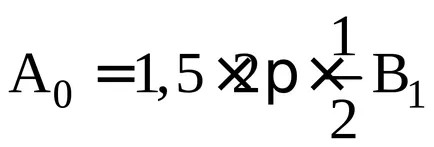


Proporțional cu pătratul amplitudinii iluminării în centrul acestui vârf secundar este de 25 de ori mai mică decât în centrul principal. Restul maximele laterale vor fi chiar mai slab, pentru că
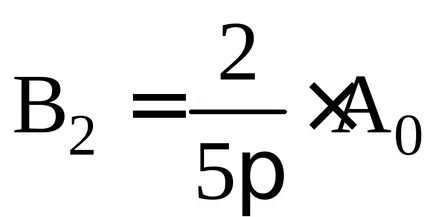
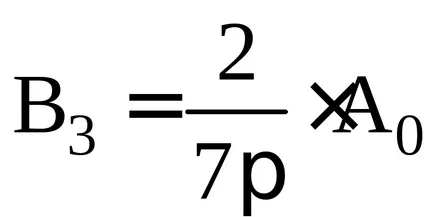
Figura arată distribuția intensității pe ecran, atunci când rețeaua de difracție în cazul N = 4 și d = 3a.

După cum se vede din figură, mai multe grinzi de interferență (din diferite sloturi) a dus la o redistribuire semnificativă a intensității luminii în comparație cu distribuția de intensitate a luminii de la o fantă (punctată în Fig. 5). Din moment ce un slot mai intens de odihnă centrale de vârf, în rețeaua de difracție, în aproape toată lumina este concentrată în vârf centrală din cauza unui decalaj, adică în
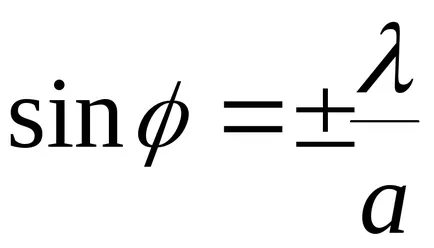
Cu o creștere a numărului total de linii (fisuri), vârfurile principale, care stau în aceleași locuri, sunt din ce în ce mai clare și mai clare.