Cum să complot graficul modulului de funcții și rădăcină

Luați în considerare │ funcției y = │ah, în cazul în care un - un anumit număr.

Domeniul funcției y = │ah │, este un set de numere reale. Figura prezintă graficele respectiv funktsiyu = │h │ y = │ │ 2, y = │h / 2│.

Este posibil să observați că graficul y = | ah | obținută din graficul funcției y = ax. în cazul în care porțiunea negativă a graficului y = ax (este sub axa x), reflectă simetric cu această axă.

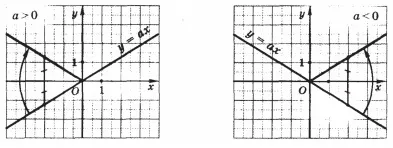
Conform programului este ușor pentru a vedea proprietățile funcției y = ax │ │.

Atunci când x = 0, y = 0 obținem, adică, face parte din graficul de origine; x = 0, avem y> 0, adică toate celelalte puncte grafice situate deasupra axei x.

Pentru valori ale lui x opuse. Valorile trebuie să fie identice; Axa Y este axa de simetrie a graficului.

De exemplu, se poate construi un grafic al unei funcții y = 3 │h │. Pentru a compara functia y = │h │i 3 y = x 3 alcătuiesc un tabel de valori pentru aceleași valori ale argumentelor.

Din tabel observăm că, în scopul de a construi un grafic al funcției y = 3 │ │h, puteți începe cu construcția graficului y = x 3. După ce stă simetric Ox spectacol axa acea parte care este sub această axă. Ca rezultat, obținem graficul prezentat în Fig.

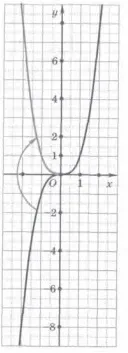
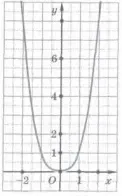
Să considerăm funcția y = x 1/2.

Domeniul acestei funcții este setul de numere reale nenegative, deoarece expresia x 1/2 are o valoare numai când x> 0.

Am construi un grafic. Pentru a compila un tabel al valorilor sale cu ajutorul calculatorului, rotunjirea valorile funcției până la a zecea.

După aplicarea punctelor de coordonatei plane și netede compușii acestora, obținem graficul funktsiiu = x 1/2.

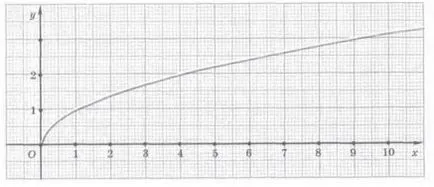
Charting ne permite formularea unor proprietăți ale funcției y = x 1/2.

Când x = 0, obținem y = 0; pentru x> 0, avem y> 0; grafic trece prin origine; celelalte puncte ale graficului situat în primul trimestru de coordonate.

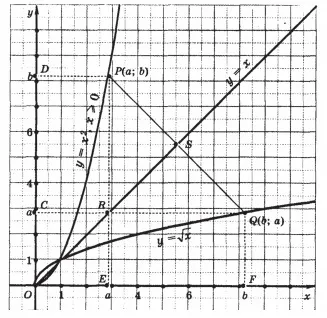
Dovada. Graficul funcției y = x 2 unde x> 0, o ramură parabolică, situată în primul trimestru de coordonate. Lăsați punctul P (a, b) - un punct arbitrar al acestui grafic. Apoi, adevărata egalitate și b = 2. Deoarece starea unui număr non-negativ, este de asemenea adevărat egalitate a = b 1/2. Aceasta înseamnă că coordonatele punctului Q (b; a) este transformată în formula y = x 1/2 în adevărata egalitate, sau în alt mod, punctul Q (b, a) aparține graficului funcției y = x 1/2.

Este dovedit că, dacă punctul M (c, d) aparține graficului funcției y = x 1/2. punctul N (d; e) aparține graficului y = x 2 unde x> 0.

Se pare că fiecare punct P (a, b) din graficul y = x 2 unde x> 0, corespunde unui punct Q unic (b, a) graficul funcției y = x 1/2 și vice-versa.

Rămâne să demonstreze că punctul P (a, b) și Q (b, a) simetric în raport cu linia y = x. Coborârea perpendicularele pe axele de coordonate ale punctelor P și Q. obține pe aceste axe punctul E (a, 0), D (0; b), F (b; 0) C (0, a). Punctul R de intersecție a perpendicularele și PE QC are coordonate (a, a) și, prin urmare, aparține liniei y = x. PRQ este un triunghi isoscel, deoarece laturile sale sunt RP și RQ │ b - și fiecare │. Y = x linie dreaptă bisects unghiul ca DOF. și unghiul PRQ și intersectează PQ segment la un anumit punct S. Prin urmare, segmentul RS bisects PRQ triunghi. Deoarece bisectoarea unui triunghi isoscel este înălțimea, iar mediana, PQ ┴RS și PS = QS. Acest lucru înseamnă că punctul P (a, b) și Q (b, a) în raport simetric față de linia y = x.

Deoarece graficul funcției y = x 1/2 simetrică funcție grafică y = x 2 unde x> 0, în raport cu linia y = x. apoi graficul y = x 1/2 este o ramură a parabolei.