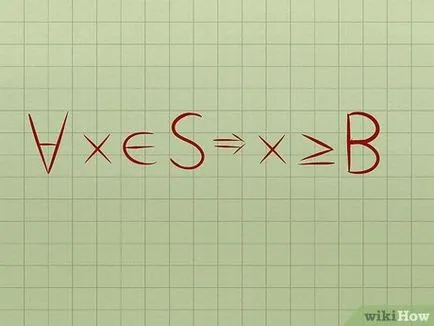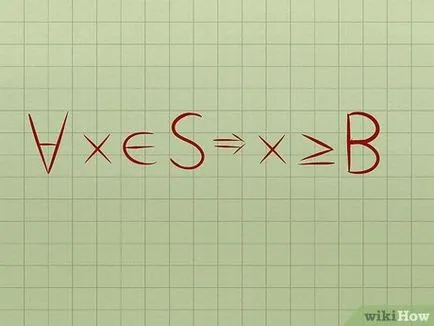Noțiunea de conceptul de limita superioară. Dacă setul de numere reale S include un număr real A ∈ R, și în care fiecare număr submulțime S mai mic sau egal cu A, atunci S este numit „top limitat“, iar A este limita superioară. Matematic, acest lucru este exprimat după cum urmează: ∀x∈S⇒x≤A. Dacă S nu are nici o limită superioară, este numit „top nelimitat“.
- Dacă există cel mai mic membru între limita superioară S, atunci acest număr se numește „limită superioară cel puțin“ sau „supremul“ set și desemnat ca cinează.
- În cazul în care S are cel puțin o limita superioară, atunci există infinit de multe limite superioare mai mari decât acest număr.
Noțiunea de conceptul de frontiera de jos. Dacă setul de numere reale S include un număr real B ∈ R și în care fiecare număr submulțime S mai mare sau egal cu B, atunci S este numită „bottom-restricționat“, iar B este inferior legat. Matematic, acest lucru este exprimat după cum urmează: ∀x∈S ⇒x≥B. Dacă S nu are limita inferioară, este numit „de jos nelimitat.“
- Dacă există cel mai mare membru al S între limitele inferioare, acest element se numește „limita de jos“ sau „infimumul“ set și desemnat ca infS.
- În cazul în care setul S are cel puțin o limita inferioară, atunci există infinit de multe limite inferioare, mai mici decât acest număr.