construcții geometrice care au fost utilizate de către meșterii antici

Problema majoră pentru arhitectul desfășurarea corespunzătoare axe longitudinale și transversale perpendiculare reciproc ale templului și construirea pătrat dom. Despre modul în care a fost efectuat această procedură, nu a fost păstrat informația. Dar este posibil să se înțeleagă ce ghidat arhitecții vechi, studiind structurile create de acestea.

Din cele mai vechi timpuri, cunoscut pentru așa-numitul triunghi „egiptean“ - un triunghi, raportul de aspect este descris de un triplu 3: 4: 5, sunt dreptunghiulare. Planurile având o proporție de 3: 4, erau palate și moșii înapoi în Egiptul antic.

Construirea unui triunghi folosind o coloană circulară, împărțită în 12 părți egale. În cazul în care cablul de tragere folosind 3 cuie așa cum se arată în figura 3a, obținem un triunghi dreptunghic. Acest lucru permite, de asemenea să construiască un triunghi dreptunghiuri și arcuri utilizate în mod obișnuit, cu un raport de 3: 4 și 4: 5 (Fig.3a).

Acesta a fost cunoscut antice și alte triplează de numere întregi. definind raportul de aspect al triunghiurilor dreptunghiulare: 05:12:13, 20:21:29, 7:24:25, 9:40:41. Cunoașterea triplu 40: 41: 9 vă permite să rezolve problema de școală (XVII sec manuscris): „Scara groapă nekoemom set 41 Cu oprire lung, și lățimea de fund în toate direcțiile până la 9 picioare și vedatelno este, colica mai sus myashe adâncime fără fund“. Conform teoremei lui Pitagora necunoscut picior cantitate (Fig.3b) se calculează cu formula :. Cel mai probabil, această sarcină necesită cunoștințe elevului de triplu (9,40,41).

O detaliere a planului bisericii a început cu construcția a două axe perpendiculare între ele. Direcția axei longitudinale a templului determinat în zori, atunci orice metodă construită axă perpendiculară la aceasta - prin intermediul compasuri serif, clin dulgher sau printr-un triunghi dreptunghic. pătrat (sau dreptunghi) După construcție construit perpendicular axe. În Georgia, pe peretele unuia dintre templele antice sculptate desen reproduce construirea pătrat pe baza axelor ortogonale (Fig. 3c). În primul rând există un cerc al cărui diametru este egal cu latura unui pătrat, semicerc apoi de același diametru ca și cercul punctelor de intersecție ale axelor sunt construite. Punctele de intersecție ale semicercuri adiacente definesc nodurile pătrat.

Toate pătrate construite și dreptunghiuri sunt măsurate în diagonală. Egalitatea diagonalelor este un semn că unghiurile figurii drepte (în timpul măsurătorilor dimensiunii diagonalelor pieselor structuri rectangulare, întotdeauna aplicate la planul). Era cunoscut de masterat și că unghiul subîntins de diametrul unui cerc - linie. Ar putea fi folosit, de exemplu, atunci când se creează un tâmplar Norma (ris.3g).

Mai mult, în cazul în care planul de a utiliza o defalcare simplu de construcție realizată prin utilizarea unui conducător și busolă, și regula proporționare că meșterii vechi posedat în perfecțiune.

Sondajele de temple antice au arătat că pentru fiecare instalație poate fi definită dimensiune modulară (original), care este baza tuturor construcțiilor ulterioare care definesc forma structurii. Toate construcțiile formează un lanț continuu, primul link este definit de o dimensiune modulară. Ca un astfel de modul poate fi o parte cupola grosime pilon al pătrat, sau chiar un fel de valoare.

Datele generalizate cuprinse în monografie K.N.Afanaseva „Construirea de arhitectura arhitecți forma drevnerumynskimi“, dă o idee despre principiile de proiectare care au ghidat constructorii bisericilor românești din secolele XI-XII.

Unele standarde ale aspectului templului interior

Dacă dimensiunea cupola "pătrat", măsurată în picioare (greacă - 308-309mm sau 295-296mm Roman) este utilizat în general dimensiuni: 25, 20, 16, 15, 12, 10 picioare. În analele dimensiuni cu ajutorul „centura Shimon“, a menționat, dar această măsură este probabil să fie de 4 picioare. În descrierea geometriei laturii templu cupola a „pătrat“ poate fi folosit ca un „modul“ - măsura inițială, care este prima verigă din lanțul de proporționalitate al tuturor elementelor clădirii.

Cuvântul „pătrat“, ne-am furnizat citate, pentru că în loc de pătrat exactă a fost adesea folosit „viu“ pătrat - aproape de piața unui dreptunghi alungit cea mai mare parte de-a lungul axei longitudinale a templului.

În descrierea constatat următoarea relație proporțională a părților cupola pătrat.

1: 1 - un pătrat exactă;

20:21 „0,95 (21:20“ 1,05) sau 09:22 „1,05 (22:21“ 0,95)

20:21 - "pătrat" ​​se extinde în direcția longitudinală (4a), 21:20 - lateral;

Versiunea cea mai simplă a descrierii acestui sistem plan de - interiorul templului, inclusiv absida - un dreptunghi, care poate fi împărțit într-un pătrat cu latura de 10, la care a fost atașat la partea de est a absida (înscris într-un 3'10 dreptunghi), iar de la vest - pronaos (ca un dreptunghi 3'10) separate printr-o porțiune de perete rugăciune sau stâlpi.

a doua versiune a aceeași descriere a planului de către - un pătrat cu latura de 10, care include un spațiu cupolă și absida, iar dreptunghiul de vest adiacente cu laturile 10 și 6. Această descriere amintește de construirea dreptunghiului „de aur“, folosind semi-pătrat în diagonală. Partea de vest a pătrat determină poziția partea de vest a pătrat dom. Dreptunghiuri cu un raport de 16: 10 = 8: 5 = 1,6: 1 și 10: 6 = 5: 3 „1.67 aproape de aur. Proporțiile de 8: 5 și 5: 3 se găsește în maeștrii antici foarte des. Domul din centrul pătrat coincide cu centrul planului. Dacă latura scurtă a dreptunghiului mic ia 6 + 1/4 = 0,625, obținem proporția foarte puțin diferită de „aur“: 16,25: 10 = 1.625 „și 1.618 6,25 10 = 0.625“ 0.618 (proporțiile de punctualitate : 0,007: 1,6 x 100 @ 0,5%). Raportul dintre lățimea laturii culoar a cupolei la pătrat: 2: 4 = 0,5. Figura 9b prezintă o diagramă aproximativă a aspectului fațadei de vest a templului.

Planul de schemă, a cărui secțiune transversală este descrisă folosind numerele 1, 3, 5, 8, 13, 21

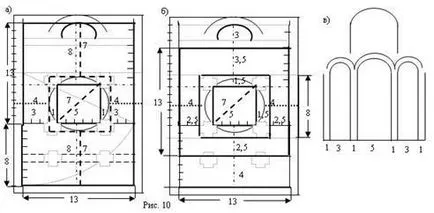
Vederea în secțiune transversală a templului este construit folosind raporturi proporționale 1: 3: 1: 5: 1: 3: 1. Magnitudinea latura cupola unui pătrat - 5 unități, grosimea pereților și coloane este egal cu 1, lățimea culoarele laterale este 3. Planul Schema poate fi desenat pe hârtie milimetrică așa cum este prezentat în figurile 10a, b. fațadă western Schema având aceste proporții este prezentată în figura 10c.

Un fel similar de planul are cea mai veche biserică păstrată la ziua de azi - (. Fondată în 1036g), Catedrala Schimbarea la Față din Cernigov. marcaje similare au multe planuri pentru „de aur“, sau aproape de proporțiile „de aur“.

Nu numai ca raport de aspect în secțiune transversală, dar, de asemenea, principalele proporții secțiuni longitudinale cât mai multe biserici au în comun. Diagrama arată că, în ceea ce privește spațiul interior al templului, inclusiv absida - un dreptunghi cu un raport de aspect de 21:13. Acesta poate fi descompusă într-un pătrat cu laturile 13:13, situat în partea de est a bisericii, și un dreptunghi cu laturile de 13: 8 în partea de vest. Partea de vest a cupola pătrat a cărui parte este în aceeași unitate de măsură egală cu 5, se află pe partea de vest a pătrat 13:13. Raportul dintre lățimea laturii culoar a cupolei unui pătrat 3: 5 = 0,6.

Vedem că proporția de dreptunghiuri, din care planul de construcție, descrise printr-o secvență de numere întregi: 1, 3, 5, 8, 13, a fost izolat 21. Această secvență (de la numerele naturale) de către arhitecți din cele mai vechi timpuri. Dacă introduceți al doilea rând numărul 2, vom obține începutul secvenței Fibonacci pe proprietățile pe care le-am descris deja.

Raportul dintre termeni succesive ale secvenței Fibonacci este foarte aproape de „aur“:

(1 + j): F = 1: 1 = 1: j '21: 13' 1.615 1 „1.618: 1 (0,003 precizie: 1,6 x 100„0,2%)

(1 + j): F = 1: 1 „13 8 = 1,625: 1„1.618: 1 (0.007 precizie: 1,6 x 100" 0.5%)

3: 5 = 0,6 »0618» j (precizie de 0.018: 0,6 x 100 „2%).

Astfel, prezenta descriere planuim proporții templu printr-o secvență de numere întregi 1, 3, 5, 8, 13, 21 asigură o bună din punct de vedere practic aproximare rațională a raportului de aspect „de aur“.

cupola centrul de pătrat în cadrul schemei este în centrul planului de dreptunghi. Figura 10b ilustrează construcția aceluiași plan de centru (se crede că defalcarea planului, în conformitate cu tradițiile, care au venit din Grecia, și anume de masterat realizate din centru). Presupunând că lățimea postului cu palete este jumătate din grosimea postului, construcția se va baza pe trei pătrate concentrice cu laturile 5, 8 și 13. Absida pe latura de est, pronaosul vest cu polii săi adiacente pătrat 13'13.

Rețineți că precizia cu care au lucrat maeștrii vechi de ordinul a 1-2%. De exemplu, pentru un pătrat cu latura a cupolei 25 de picioare (≈7,7m) lungime diagonală este de aproximativ 11m, iar diferența în lungimile diagonalelor 2 este 20cm. Lungimea diagonalei unui dom pătrat diferă cu aproximativ 2%. Diferența în lățimea culoarelor 3cm deși mărimea lor este de aproximativ 150 cm (2%), etc.

Pentru a obține proporțiile de nord și cea sudică, vom lua raza absidei pentru o estimare aproximativă. De obicei, diametrul absidei o cantitate de 2 lame inferioare est a cupolei unui pătrat. Deci, presupunem că raza absida egală cu 2 unități. Se termină stâlpi absida cu lame înlocuirea peretelui de est și acest lucru ne dă lungimea templului din exterior fără apsides de 20 de unități (21-2 + 1). partiționarea astfel, nord și partea de sud a casei de la est la vest la circuitul prezentat în figurile 10a, b, poate fi descrisă ca proporția de 1: 2: 1: 4: 1: 5: 1: 3: 1: 3: 1.

În schemele de tobă noastre iau cel mai simplu exemplu de realizare, atunci când diametrul exterior al tamburului este egală cu latura mică a cupolei într-o sumă pătrată cu cei doi piloni. Apoi, circuitul 1 2 1 4 1 2 1 diviziune umăr - cilindru - umăr descrie proporția de 3: 6: 3 = 1: 2: 1, deoarece lungimea brațului a peretelui tamburului exterior la marginea peretelui templului este grosimea peretelui, plus lățimea culoarului, t.e.1 + 2 = 3, iar diametrul tamburului este un pol doi plus grosimea laturii cupola unui pătrat, adică, 1 + 4 + 1 = 6. Pentru schema 1 3 1 5 1 3 1 4 rația spirelor: 7: 4. Aceste diagrame arată modul în care alegerea schemei se reflectă în aspectul clădirii.

Construcția „de aur“ plan de conducător și compasul

Am dat două construcții care pot fi realizate doar pe hârtie milimetrică. Aceste scheme sunt baza planurilor de mai multe temple.

Construi planul diagramă care cuprinde raporturi iraționale, utilizând o riglă și compas - în interiorul raportului dintre lungimea templului total (s absidă) pentru lățime nu este aproape de „aur“, și tocmai „de aur“ (F 1 = 1: j @ 1618: 1 @ 1: 0,618), iar cupola sa de pătrat este alungită în direcția longitudinală și are un raport de aspect egal (raport de aur caracteristică - proporția stăpânilor antice bine cunoscute).

Construim pe un pătrat în carouri de hârtie. În continuare, se trage, astfel încât dimensiunea longitudinală a unui „pătrat“ a fost în dimensiunea mai transversală. Această construcție se poate realiza folosind semi-pătrat în diagonală sau cu un șubler, iar soluția este de 1,5 ori mai mare de pătrat (Fig. 11b). Construcția poate începe din partea de jos în sus (Figura 11a) sau din centrul (Fig. 11c).

Construcția centrului busolei se va întinde simultan în direcția longitudinală în timp pentru a ajunge la axa transversală a templului în afara granițelor „miezului“, care este înscrisă în cupola și coloanele unui dreptunghi. Proportional relații „de bază“ sunt determinate din construcția dreptunghiului „de aur“ prin diagonală semi-pătrat (fig. 11c).

Formulele de a planifica o parte mică cupola de pătrat este luată ca unitate, toate celelalte dimensiuni sunt exprimate în valoarea acțiunilor, astfel încât acesta servește ca un modul, stând la începutul lanțului de construcție și joacă rolul unității proporțional cu raportul. Dacă presupunem că grosimea de pol egală cu un sfert de o parte pătrat a cupolei, lățimea lamei este aproximativ egală cu un sfert din grosimea stâlpului, grosimea pol, în total cu palete este de aproximativ 1/4 + 1/4 x 1/4 = 0,25 + 0,0625 = 0,3125. Și în construcția cu un șubler j / 2 „0.309. În consecință, latura mică + 2 (palete + post) „1 + j, pe care le-am reprezentat în fig. Dacă distanța de la limitele nucleului la pereții laterali ai templului este de 0,5, lățimea templului în interior este 2 + j. Dimensiunile longitudinale ale interiorului templului este definită după cum urmează: distanța de la granița de est a domului pătrat la granița de est a interiorului cupola templului este egal cu diagonala unui „pătrat“, adică de 1,5, iar distanța de la granița de vest a domului „pătrat“ pe peretele vestic al templului aceeași lățime de bază, adică, 1 + j. Aceste construcții sunt ușor realizate folosind o busolă și un plan devine clasic „de aur“ raport de aspect - ea constă dintr-un pătrat cu laturile 2 + j și un dreptunghi cu laturile 2 + j 1 + j, raportul dintre laturile planului dreptunghiului, astfel, egal cu (3 + 2j ) :( 2 + j) = 1: j = F: 1.

construcția noastră oferă o diviziune transversală interioară în conformitate cu proporția de 0,5: j / 2: 1: j / 2: 0,5 = 1: j: 2: j: 1 (lățimea culoarului este egală cu jumătate din grosimea / 2 zone coloana j Steaua a laturii cupola a pătrat). side Dome unui pătrat, în acest caz, împarte o axă transversală în raport cu: (1 + j): 2 (1 + j) = F 2: P = F / 2: 1: F / 2 = 1: 2j: 1, care poate fi exprimat în formă numerică: 0,809: 1: 0,809 @ 1: 1,236: 1.

abordare rațională a acestui plan va fi un plan: cupola „pătrat“ 4'4,5; grosimea stâlpului 1, lățimea 1/4 a lamei, adică lățimea „miez“ de 6,5 ..; lățime interioară 10,5; distanța de la latura de vest a domului pătrat la „miezul“ al peretelui vestic aceeași lățime, adică, 6.5; distanta de la partea de est a cupola „pătrat“ la limita estică a interiorului bisericii, inclusiv absida, cupola este egală cu diagonala unui „pătrat“, adică 6; lungimea totală a interiorului templului inclusiv absidă, 6,5 + 4,5 + 6 = 17; partea de vest a pătrat cupola se afla pe partea de vest a pătrat 10,5'10,5. Dacă toate aceste numere este înmulțit cu 2, obținem un număr de 8, 13, 21, 34 din șirul lui Fibonacci, care ofera un „aur“ raport de aspect.

Așa cum am discutat anterior scheme raționale ale domului centrul pătrat în centrul axei longitudinale. În această schemă, o construcție care corespunde cu un șubler, nu este așa - distanța de la centrul cupolei „pătrat“ la peretele de est (Absida perete) este egal cu 6 + 2,25 = 8,25, iar la peretele de vest 6,5 + 2 25 = 8,75, adică 0,5 (½ grosime pilon) decât la peretele vestic.

Această schemă de circuit corespunde aproximativ la planul Assumption Catedrala Eletski mănăstire din Cernigov conținute în cartea Sheveleva Shaping“, iar schema de descriere planul de scara 1:50 dat în monografia Afanasyeva. Pentru o cantitate mică din partea templu Dome „pătrat“ este 622sm (y Sheveleva 622sm, y Afanasyeva 616-618sm) Grosimea coloanei este de aproximativ 1/4 din această valoare, lățimea lamei este de aproximativ 1/4 din grosimea coloanei (total 192cm), lățimea în interiorul templului este 1624sm, lungimea interiorului templului este 2655sm. Astfel:

Dacă luăm în considerare grosimea coloanei unitate (aproximativ 155cm), latura mică a domului pătrat este egal cu 4, lățimea miezului este 1006: 155 „de 6,5, egală cu lățimea interioară 1624 155“ Lungime 10.5 2655 Interior: 155 „17.

Suma care poate fi cu ușurință exprimate prin dimensiunile diferitelor părți ale structurii, numit un modul. În descrierea noastră un rol modul de circuit a fost jucat de amploarea cupolei sau pătrat pilon grosime.

Proporțiile planului obținut prin măsurarea de-a lungul pereților exteriori, datorită pereții templului sunt diferite de interne și revizuite aici sunt o relație proporțională simplă, care poate fi descrisă de relațiile integrale: 5: 4, 3: 2, 6: 5.

Noi nu am atins și aproape că nu va aborda aspecte legate de dimensiunile verticale și proporțiile templului. Remarcăm doar că a existat o regulă conform căreia dimensiunile verticale ale structurii sau direct preluate din planul său sau de a comunica cu dimensiunile orizontale ale unei relații proporționale simplu - bun venit, foarte convenabil din punct de vedere al tehnologiei. Raportul proporțională între dimensiunea verticală și orizontală și verticală între articula - aceasta este din nou cele mai simple relațiile raționale și proporțiile, generează o diagonală de pătrat și semi-pătrat, și derivații acestora.