Conducerea reprezentarea grafică a funcției - rezolvarea problemelor, controlul

Conducerea funcții plotare

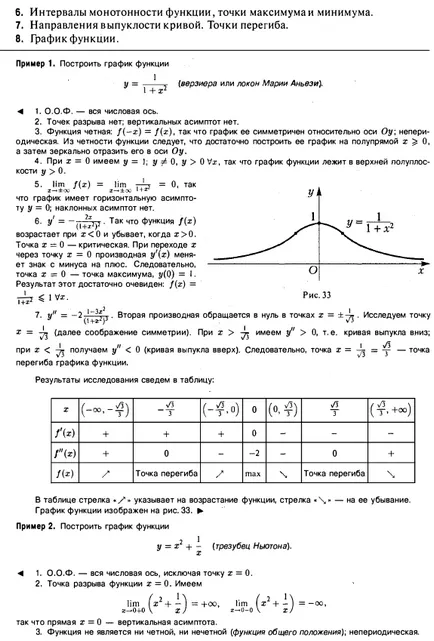
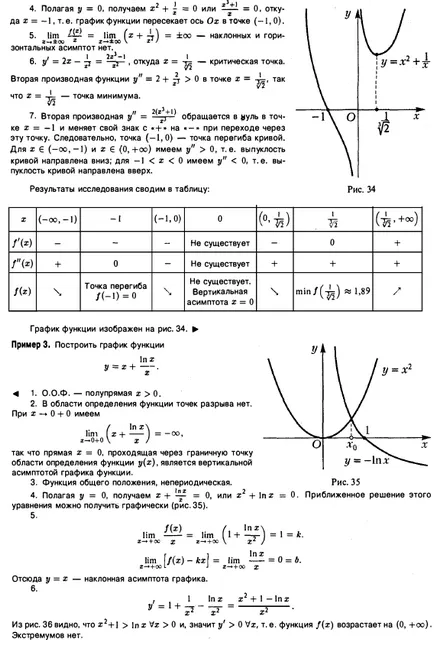
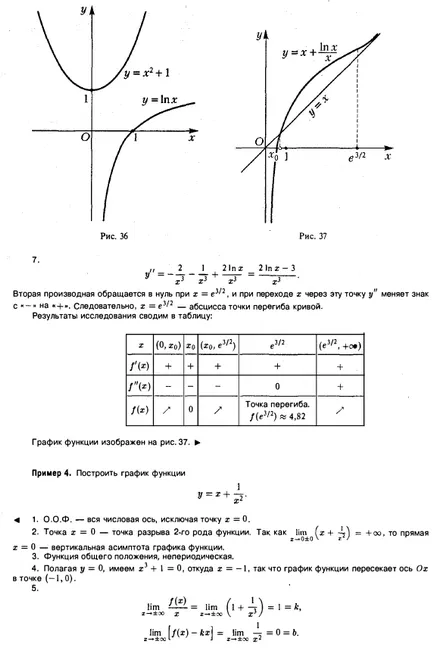
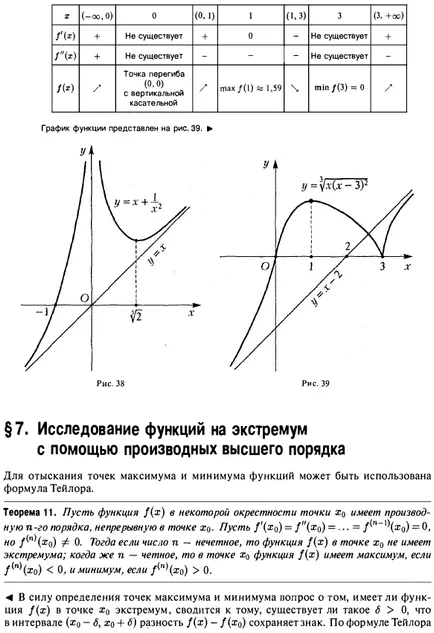
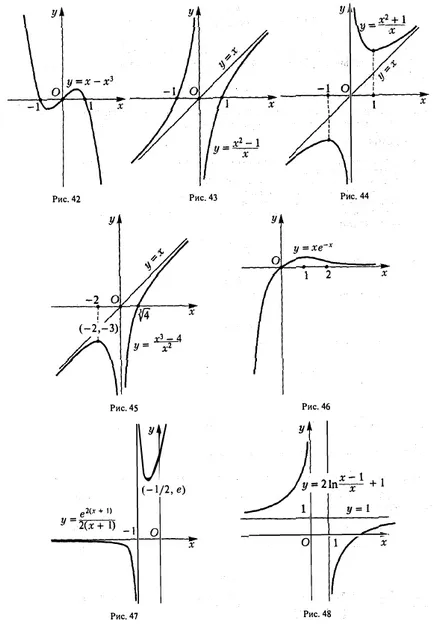
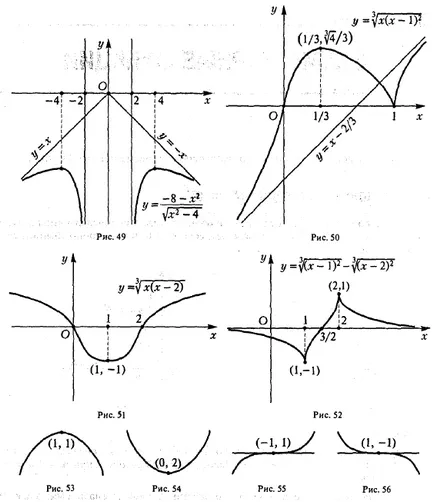
Una dintre posibilele scheme și studii de construcție caracteristici program ce defalcate în următorii pași pentru rezolvarea problemei: 1. Domeniul funcției (O.O.F.). 2. Punctul de discontinuitate al caracterului lor. asimptotă verticală. 3. Paritatea este impar, funcția de frecvență. 4. Punctele de intersecție ale graficului cu axele de coordonate. 5. Comportamentul funcției la infinit. asimptotă orizontală și oblică. 6. Intervale de funcții monotonie, puncte maxime și minime. 7. Directii curba convexă. punct de inflexiune. 8. Funcția Program. Exemplul 1. Plot funcția y = 1. (vereiora sau ondularea Aneei Mary). - întreaga axă reală. 2. puncte de pauză acolo; asimptotă verticală acolo. 3. Funcția este chiar. astfel încât graficul său este simetrică în raport cu axa Oy \ aperiodice. Din funcția de paritate, care Doștat ^ o construi programul ei pe jumătate de x O, și apoi flip-l la axa y. 4. Când x = 0, avem Oh, astfel încât graficul funcției se află în semiplanul superior y> 0. Schema de construcție a graficului funcțiilor privind Investigarea valorii extreme prin utilizarea instrumentelor derivate de ordin superior ale rădăcinilor metodelor ecuațiilor de calcul de acorduri și tangente că graficul are o asimptota y orizontal = O, panta asimptota acolo. De atunci crește și scade atunci când funcția când. X = 0 - critic. La trecerea prin punctul x = x 0, derivata y „(x) își schimbă semnul său de la plus la minus. În consecință, punctul x = 0 - punctul maxim, y (Q) = I. Acest rezultat este destul de evident: / (x) = T ^ IV *. Derivata a doua este zero la x =. Investigați punctul x = 4- (în continuare cont de simetrie). Dacă avem. curba convexă în jos; la obținem (curba convexă în sus). În consecință, punctul x = - - punctul de inflexiune al funcțiilor graficului. Rezultatele studiului sunt prezentate pe scurt în tabelul: max punct de inflexiune punct de inflexiune B • La săgeata de masă „indică creșterea funcției, săgeata“ \ „- pentru ao micșora. Diagrama funcției prezentată în Fig. 33. Exemplu grafic funcția 2. Build (tridentul Newton). - întreaga axă reală, cu excepția punctului 2. Punctul de discontinuitate funcții. Avem, astfel încât linia x = 0 - asimptota verticală. 3. Funcția nu este nici chiar nici nui funcția generică [), un non-periodice. Presupunând că obținem graficul axa x intersectează punctul (-1,0). înclinat și asimptotă orizontală acolo. dintr-un punct critic. Derivata a doua a funcției în punctul. astfel încât x = - un punct minim. Al doilea instrument financiar derivat devine uul la punct și își schimbă semnul său atunci când trece prin acest punct. Prin urmare, punctul de - punctul de inflexiune. Pentru curba descendentă a) ne-am îndreptat e convexitate .; Trebuie să -I. curba convexitate îndreptată în sus. Rezultatele studiului sunt prezentate pe scurt în tabelul: Nu există Nu există nici un punct de inflexiune nu există. Asimptotă verticală derivatul Thoraya dispare la x = e / 2. iar când x trece prin punctul y „Modificări semn în consecință, - abscisa punctului de inflexiune al rezultatelor studiului sunt prezentate pe scurt în tabelul: Funcția program punct de inflexiune este prezentată în Figura 37. Exemplul 4. Se construiește graficul întregii axei reale cu excepția punctului punct ... ruptura a 2-un fel de funcție. deoarece Km. asimptota dreaptă verticală a graficului funcției. funcția generică, un non-periodice. y Punând = 0, avem. unde deci graficul funcției traversează axa x la punctul aceea, graficul asimptota înclinat din starea etaj ceai - punctul critic al doilea derivat y „= D> 0 peste tot în domeniu, în special, la punctul -. Punctul minim al funcției. 7. Așa cum. apoi peste tot în domeniul definiției nervurii a graficului său este îndreptată în jos. Rezultatele studiului sunt prezentate pe scurt în tabelul: Nu există Acolo. x = 0 asimptota Funcția program vertical este prezentată în Fig. Exemplul 5. Se trasează întreaga funcție axa reală. 2. continuă peste tot. Nr asimptotă verticală. 3. Dispoziții generale aperiodice. 4. Funcția dispare la 5. Astfel, graficul funcției are un derivat asimptota înclinat dispare în momentul în care există. La trecerea prin punctul x), instrumentul derivat nu se schimbă semnul, astfel încât punctul x = 0 nu extremelor. La trecerea prin punctul de x derivat) se schimbă de la semn „+“ semnifică o funcție are un maxim. La trecerea prin punctul x = 3 x (x> I) derivat y „(x) își schimbă semnul t. E. In Tochs x = 3, funcția are un minim. 7. Găsiți derivata a doua plotting funcții de circuit funcția pe extremum Studiu folosind metode derivați de ordin superior de calcul rădăcinile acorduri și tangente doilea derivat y „(x) nu există în punctul x = 0 și x trece prin punctul x = 0, y“ modificări semn de la • + • la astfel încât punctul (0,0) al curbei - punctul de inflexiune cu o tangentă verticală. La punctul x = 3 nu inflexiune a graficului. De-a lungul semiplanul x> 0 convexitatea îndreptată curba ascendentă. Rezultatele studiului sunt prezentate pe scurt în tabelul: Există Există există Nu există nici un punct de inflexiune (0.0) cu un grafic tangenta vertical al funcției prezentate în Fig. 39. §7. funcțiile de investigare prin intermediul unui extremum al derivaților de ordin superior cu formula Taylor poate fi utilizat pentru identificarea punctelor maxime și minime ale funcțiilor. Aceasta teorema. Fie funcția / (x) într-un cartier al xq are un derivat de ordinul n, continuă HO- Să presupunem că la punctul 0. Dacă numărul n - este impar, atunci funcția f 0, care este în intervalul. diferența - / (X0) își păstrează semnul său. Formula lui Taylor prin ipoteză. apoi de la (1) obținem 1ousloviyu / (n * (z) este vtochkego continuă și, prin urmare, F siluustoychivosti Naka funcții continue există astfel încât intervalul () este nemodificată, și coincide cu semnul / (n) (o) ia în considerare cazurile posibile ..: 1) n - este un număr chiar și / Apoi, prin urmare, prin (2). Prin definiție, acest lucru înseamnă că primul punct este punctul de minim al funcției / (g). 2) n - și chiar. Apoi, avem i cu ea, și, prin urmare, primul punct este aceasta: raza maxima a functiei / (g). 3) n - număr impar / - Atunci pentru x> x0> semn udet coincide cu semnul / (n) (w) și când r-lea este opusul. De aceea, 1RI semn arbitrar mic de diferența 0 / (z) - / (th) nu este același toate 1lya xe (th - 6 th + £). Prin urmare, în acest caz, funcția / (z), la punctul de zhstremuma are. Exemplu. Luați în considerare funcția h este ușor de văzut că x = 0 este un punct critic al ambelor funcții. Pentru y funcția = x4 din primul derivat non-zero la punctul x = 0 este derivata de ordinul a 4: Astfel, în cazul în care n = 4 - și chiar. În consecință, la x = 0, y = funcția x4 are un minim. Pentru functia y = x> a primei nenulă la x = 0, derivatul este un derivat al treilea ordin. Deci, în acest caz, n = 3 - impar și la punctul x = 0 al funcției y = x3 are un extremum. Notă. Cu ajutorul formulei Taylor se poate dovedi următoarea teorema, condiții suficiente pentru exprimarea punctului de inflexiune. „Eorema 12. Fie / (z) într-un cartier al proizvodp punctul Z0 are doua ordine continuă în punctul XQ. Să. dar / (n) (xo) ^ 0. Apoi, dacă n - impar, Mo (x0, f (Ho)) este un punct de inflexiune a graficului y = f (x). Cel mai simplu exemplu este furnizat de funcția. §8. Metode de calcul ale rădăcinilor corzilor și problema tangențială este de a găsi rădăcinile reale ale ecuației presupune că sunt îndeplinite următoarele condiții: 1) funcția f (x) este continua pe intervalul [a, 6]; 2) numărul / (a) și f 0, f „(x)> 0 în intervalul [a, 6) (Fig.41). Join punctele A (a / (a)) și B (b, f (b )) a B. coardă Acest segment de linie trece prin punctele a și B, a cărui aj ecuație punct în care coarda AB intersectează axa x, între și (și este o aproximare mai bună decât o. Setarea în (2) y = 0 , ne găsim din Fig. 41 este ușor de văzut că punctul de un \ va fi întotdeauna situat pe partea din care semnele f (x) și f „(x) sunt opuse. acum trage o tangentă la curba y = / (x) la punctul B ( b, f (b)), t. e. în capătul arcului AB ^, unde f (x) și / „(i) au același semn. Acesta este un important condiție: fără a respecta punctul de intersecție al tangentei cu Ox nu poate da o aproximare a rădăcinii punctului b \ dorit, în cazul în care tangenta traversează axa x, este situat între £ și b sunt pe aceeași parte ca și cele 6, și este cea mai bună aproximare a. . tangentă decât L dată de ecuația Punerea acest lucru în (3) y = 0, găsim L \: schema de construire a graficului funcțiilor de studiu asupra extremum folosind metode derivați de ordin superior de calcul rădăcinile acorduri și tangente Astfel, vom lăsa eroarea absolută de ca. zheniya cu rădăcini dat £ în avans. Pentru eroarea absolută a valorilor aproximative ale aj și 6, rădăcina poate lua o valoare de £ | 6i - ai |. Dacă această eroare este mai mult decât acceptabil, apoi a lua un segment al sursei, găsim următoarele aproximări ale rădăcinii în cazul în care. Continuând acest proces, obținem două secvențe sunt valori aproximative și secvențe ale limitelor repetitive și limitate și, prin urmare, au. Să Se poate demonstra că în cazul în care condițiile prevăzute anterior sunt singura rădăcină a ecuației 1 / Exemplu. Găsiți root (ecuația z2 - 1 = 0 în intervalul [0,2). Rezultatul este evident. Să încercăm să-l prin acorduri. Funcția / (x) = x2 - 1 1) este continua pe intervalul [0, 2); păstrează semnul în intervalul [0, 2]. Astfel, toate condițiile care asigură existența unei singure rădăcină (ecuația x2 - .. 1 = 0 în intervalul [0, 2] și metoda ar trebui să funcționeze 8 cazul nostru a = 0, b = 2. Când n = I (4) și (5), suntem la n = 2 obținem care oferă o aproximare la valoarea exactă a rădăcinii (cu un vocabular eroare absolută construi funcții grafice: Găsiți cea mai mare și cea mai mică valoare a funcțiilor la intervale predeterminate: Examinați comportamentul în vecinătatea funcțiilor specificate puncte folosind instrumente derivate de ordin superior: Răspunsuri