Conceptul integrala definită

Definite integral de la b la o funcție continuă y = f (x), definită pe intervalul [a, b]. numita creștere primitivă F (x), pentru funcția, adică,

Numerele a și b sunt numite limitele inferioare și superioare ale integrării.

Sensul geometric al integrala definită:
Ploschat S trapez curbiliniu (programul firury mărginit continuu pozitiv asupra intervalului [a, b] Funcția y = f (x), axa OX și liniile drepte x = a și x = b se calculează cu formula:

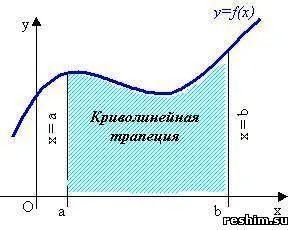
Semnificația geometrică a definit integralei. Conceptul de op-
definiteness integrantă a introdus în așa fel încât, în cazul Ko
Funcția y = f GDS

numeric egală cu aria de sub curba S y = f (x) pe [a, b]

Intr-adevar, tinde max (jos i) delta (jos i) la zero rupt în mod arbitrar aproape de sursa
curbă și aria de sub linia poligonală trece în aria de sub curbă.
Luând în considerare acest lucru, putem specifica valoarea unora
integralelor folosind formula planimetric cunoscută
pentru zonele de figuri plane. De exemplu,

(Prima parte integrantă - zona pătrată cu o latură a unui unificat
Lungimea -boundary; al doilea - zona triunghiuri dreptunghiulare
Single, două picioare a cărei unitate de lungime; a treia - zona de
sfert de cerc de rază unitate; Noi oferim cititorului în Ka-
onoruri exercitarea de a face desenele necesare auto
TION.)
De notat că ecuația (11.3) este compatibil cu geometric
semnificația integrala definită: atunci când segmentul invariante
Integrarea este contractat la un punct, cifra se micșorează sub curba
segment, din care suprafața este egală cu zero, deoarece acest domeniu
dreptunghi, din care o parte este egală cu zero.