Componenta tangențială a accelerației

t. e. egal cu derivata prima dată a vitezei modulului, determinând astfel viteza ratei de schimbare a modulului.

Am găsit a doua componentă de accelerare. Să presupunem că punctul B este suficient de aproape de punctul A, deci Ds poate presupune un arc de cerc de rază r, care diferă puțin de la coarda AB. Apoi, din similitudinea dintre AOB triunghiuri și EAD trebuie DVN / AB = v1 / r, dar din moment ce AB = v Dt, atunci

În limita obținem.

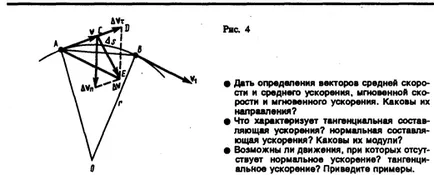
Deoarece, unghiul EAD tinde la zero, iar din triunghiul-EAD ravnobed renny, ADE unghiul dintre v și DVN tinde să direcționeze. Prin urmare, atunci când vectorii DVN și v sunt reciproc perpendiculare. Fiscal ca un vector de viteză direcționată tangențial la traiectoria, vectorul DVN. perpendicular pe vectorul de viteză îndreptată spre centrul de curbură. A doua componentă a accelerației este egală cu

numita componentă accelerație normală direcționată de-a lungul normalei la traiectoria centrului de curbură (deci este numită accelerare centripete).

accelerarea completă a corpului este suma geometrică a componentelor tangențiale și normale (Figura 5):

Astfel, componenta tangențială a accelerației caracterizează viteza ratei de schimbare a modulului (tangențial la calea), iar componenta normală a accelerației - viteza ratei de schimbare în direcția (spre preț-cale curbura muncii).

În funcție de componentele tangențiale de accelerare și normale ale mișcării-set pot fi clasificate după cum urmează:

1), AN = 0 - mișcare uniformă rectilinie;

2) AN = 0 - rectilinie uniform accelerată mișcare. In acest tip de mișcare

Dacă t1 inițial de timp = 0, iar v1 inițial viteza = v0. apoi, ceea ce denotă t2 = t și v2 = v, obținem din

Integrarea această formulă în intervalul de la zero la un punct arbitrar în timp t, constatăm că lungimea traseului parcurs de punct, în cazul mișcării uniform accelerate

3) AN = 0 - mișcare rectilinie cu accelerație variabilă;

4) AN = const. În cazul în care viteza nu se schimbă în valoare absolută, dar schimbări de direcție. Din formula o = v 2 / r, rezultă că raza de curbură trebuie să fie constantă yannym. Prin urmare, mișcarea circulară este uniformă;

5) - mișcarea curbilinie uniform;

6), - o mișcare uniform accelerată curbat;

7) - mișcare curbilinie cu accelerație variabilă.

§ 4. Viteza unghiulară și accelerația unghiulară

Să considerăm un corp rigid, care se rotește în jurul unei axe fixe. Apoi, punctul de acest corp-DEPARTAMENTUL LARG ar descrie un cerc de raze diferite ale căror centre se află pe axa de rotație. Să presupunem că un punct se mișcă de-a lungul unui cerc cu raza R (fig. 6). Poziția sa, după un interval de timp Dt cere unghiul D. elementar-Nye (infinitezimale) rotații pot fi considerate ca vectori (ele reprezintă sau Xia). vector modulul egal cu unghiul de rotație și direcția coincide cu direcția de deplasare înainte a vârfului șurubului, al cărui cap este rotit în direcția de deplasare a unui punct de pe circumferință, adică șurub dreapta podchinyaetsyapravilu (Fig.6). Vectori ale căror direcții asociate cu vectorii numita iliaksialnymi direcție vayutsyapsevdovektorami rotație. Acești vectori au definit puncte reprezentate de aplicare: acestea pot fi depuse din orice punct al axei de rotație.

viteza unghiulară este o mărime vectorială, care este egal cu primul derivat al unghiului de rotație a corpului în timp:

Vector este direcționat de-a lungul axei de rotație a regulii șurubului dreptaci, adică precum vectorul (Figura 7). Dimensiunea vitezei unghiulare dim w = T - 1, iar unitatea sa - pentru ro pe secundă (rad / s).

Viteza liniară a punctului (vezi. Fig. 6)

Formula vector poate fi scris ca un produs vector al vitezei liniare:

In acest produs vectorul unitate, prin definiție, egală, și coincide cu direcția de mișcare de translație a șurubului din dreapta așa cum se rotește pe k R.

Dacă (= const, rotirea uniformă poate fi caracterizată și perioada de rotație T -. Momentul în care moment face o rotație completă, adică se rotește 2p Deoarece intervalul de timp Dt = T corespunde = 2p, atunci = 2p / în cazul în care T.

Numărul de rotații complete ale corpului cu o mișcare uniformă a acestuia într-un cerc, într-o unitate de timp se numește viteza:

accelerația angulară este o mărime vectorială egală cu prima derivată a vitezei unghiulare în raport cu timpul:

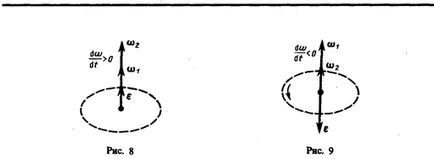
Când corpul se rotește în jurul unui vector de accelerație unghiulară axă fixă ​​este direcționată de-a lungul axei de rotație în direcția vitezei unghiulare vectorului incremente elementare. vector de mișcare accelerată aceeași direcție ca și vectorul (Figura 8), cu încetinită-cotata - sunt contra acesteia (Figura 9).

Componenta tangențială a accelerației

Componenta normală a accelerației

Astfel, legătura dintre linia (.. S lungimea căii parcurse de punct de-a lungul cercului arc de rază R. viteza lineară v, accelerația accelerației tangențial) și valorile unghiulare (rotația unghiului j, viteza unghiulară w, unghiular accelerație e) se exprimă prin următoarele formule:

În cazul punctelor de mișcare uniform accelerată circumferențial (e = const)

unde w0 - viteza unghiulară inițială.