cifrele de conversie

I. Conversia - deplasarea fiecărui punct al figurii într-un fel, și obținerea o formă nouă.

II. Tipuri de conversie în spațiu ca, mișcarea homothety.

factor de conversie F se numește o transformare de similaritate, această transformare dacă distanța dintre punctele sunt schimbate în același număr de ori, adică, pentru oricare două puncte X și Y forme F și punctul X 'Y' forma F 'în care se mișcă, x'y' = k * XY.

scalarea proprietăți: 1. Similarity transformă linii în linii, jumătăți de linii - în jumătăți de lungimi - în segmente.

2. Similaritatea păstrează unghiurile dintre jumătăți de linii

Similitudinea transformă planurile în plan.

Doua figuri se spune că sunt similare, dacă acestea sunt transformate în una de alta printr-o transformare de similaritate.

Dil - transformare mai simplă în raport cu centrul O k coeficientul homothetic. Această transformare, care transformă un punct arbitrar X „OX raze, astfel încât OX“ = k * OX.

homothety de proprietate: 1. homothety transforma ia orice plan care nu trece prin centrul de dilatare într-un plan paralel (sau în sine, atunci când k = 1).

Dovada. Într-adevăr, lăsați O - homothety centru și - orice plan care nu trece prin O. Luați în considerare orice linie AB în planul a. Omotetie trebuie să punctul A la punctul A 'pe grinda OA și punctul B la punctul B' pe OB Rază și OA '/ k = OA, OB' / OB = k, unde k - coeficientul de dilatare la. Rezultă din similitudinea triunghiuri AOB și A'OB“. Din asemănarea triunghiurilor să fie egale unghiurile corespunzătoare OAB și OA'B „ceea ce înseamnă că liniile paralele AB și A'b“. Să luăm acum o altă linie de curent alternativ în planul A. Se merge cu homothety și o linie paralelă A'C“. Atunci când a considerat avionul homothety apereydet într-un plan „, care trece prin liniile de A'b« A'C». Deoarece A'b „|| AB și A'C“ || AC, atunci teorema pe două linii care se intersectează cu un plan paralel cu, respectiv, linii diferite plane care se intersectează, o și o „sunt paralele cu planul, după cum este necesar.

Mișcarea - transformarea o cifră la alta, dacă se păstrează distanța dintre puncte, și anume traduce oricare două puncte X și Y ale unei figura în ceea ce privește un alt Y figura X., astfel încât Y XY = X

Caracteristici circulație: 1. Punctele de pe linie, atunci când mișcarea este convertită în puncte pe o linie dreaptă, și proceduri stocate pentru dispunerea lor reciprocă. Acest lucru înseamnă că, în cazul în care A, B, C, situată pe linia, trece la punctul A1, B1, C1. Aceste puncte se află, de asemenea, pe o linie dreaptă; în cazul în care punctul B se află între punctele A și C, atunci punctul B1 se află între punctele A1 și C1.

Dovada. Să punctul linia B AC se află între punctele A și C. Noi arată că punctele A1, B1, C1 sunt coliniare.

Dacă punctul A1, B1, C1 nu se găsește pe linia, ei sunt vârfurile triunghiului. Prin urmare, A1C1

Avem o contradicție. Prin urmare, punctul B1 se află pe linia A1C1. Prima declarație a teoremei.

Noi acum arată că B1 se află între A1 și C1. Să presupunem că A1 se află între punctele B1 și C1. Apoi a1b1 + A1C1 = B1C1, și, prin urmare, AB + AC = BC. Dar acest lucru contrazice inegalitatea AB + BC = AC. Astfel, punctul A1 nu se poate situa între punctele B1 și C1.

În mod similar demonstrăm că punctul C1 nu se poate situa între punctele A1 și B1.

1. Din cauza celor trei puncte A1, B1, C1, unul se află între celelalte două, atunci acest lucru poate fi doar un punct B1. Teorema este demonstrată.

2. Atunci când conduceți direct în linii drepte, jumătăți de linii - în jumătăți de lungimi - în segmente

3. În timpul mersului păstrează unghiurile dintre jumătățile de linii.

Dovada. Să AB și AC - două jumătăți de linii care provin de la punctele A, nu se află pe o linie dreaptă a acestuia. Când conduceți jumătățile de linii de du-te în unele jumătăți de linii de a1b1 și A1C1. Deoarece mișcarea păstrează distanța, triunghiurile ABC și A1B1C1 sunt egale, pe baza celui de al treilea egalității de triunghiuri. Din egalitatea de triunghiuri să fie unghiuri egale BAC și B1A1C1, după cum este necesar.

4. Propunerea se traduce într-un plan plan.

Să ne dovedesc această proprietate. Să o - un plan arbitrar. Notă pe acesta orice trei puncte A, B, C, nu se află pe o singură linie. Prin intermediul lor un „plan.

Ne arată că, atunci când mișcarea considerată într-un plan intră într-un „plan.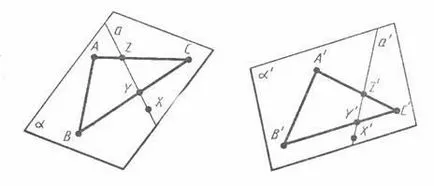

Fie X - punct aleatoriu în plan o. trage prin ea orice linie într-un plan a, ABXC intersectează triunghiul în două puncte Y și Z. directe și pentru a muta în timp ce se deplasează într-o anumită linie a“. Punctul Y și Z se va muta linia un punct de Y „și Z“, aparținând triunghiului A'B'C „și, astfel, un avion“.

Deci, conduce o „minciună într-un plan." Punctul X în timp ce se deplasează în punctul X „linia de o“, și, prin urmare, planul unei“, după cum este necesar.

În spațiul, cât și pe plan, cele două cifre care se spune că sunt egale dacă sunt combinate circulație.

III. Tipuri de Motion: simetrie în jurul unui punct de simetrie în raport cu linia de simetrie în raport cu rotația plan, mișcare, translație paralelă.

Simetria în ceea ce privește punctul

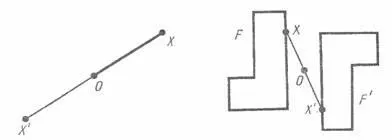
Fie G - punct fix și X - punct aleatoriu în avion. Ne amâna continuarea OX segment al punctului OX O segment“, egal cu OX. Punctul X „se numește punctul X simetric în jurul unui punct O. Punctul simetric punctul O, punctul în sine este O. Este evident că un punct simetric la punctul X“, este un punct de X.

Cifrele de conversie în figura F F „în care fiecare punct X se mută la un punct X“, simetric în raport cu un punct dat O, numita transformare punct de simetrie în raport O. În această figură F și F „sunt numite simetric cu punctul O.

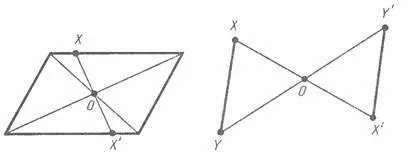
Dacă transformarea simetrie în raport cu punctul O F are nevoie de o formă, se numește central-simetrică și punctul O se numește un centru de simetrie.

De exemplu, un paralelogram este central figura simetrică. Centrul său de simetrie este punctul de intersecție al diagonalelor.

Teorema: Conversia de simetrie în raport cu un punct de mișcare.

Dovada. Fie X și Y - două puncte arbitrare ale figura F. de conversie simetrie în jurul punctului O le transformă în X „și Y“ punct. Luați în considerare triunghiuri XOY și X'OY“. Aceste triunghiuri sunt egale, pe baza primului triunghi egalității. Acestea au inclus unghiurile O sunt atât pe verticală și OX = OX „OY = OY“, prin definiție, o simetrie în raport cu punctul O. Din egalitatea triunghiurilor trebuie să fie egalitatea armelor: XY = x'y“. Aceasta înseamnă că simetria în ceea ce privește punctul O este mișcare. Acest lucru dovedește teorema.

Simetria în raport cu o linie dreaptă

Să g - linie fixă. Ia un punct X și AX arbitrar n picătură linie perpendiculară g. În continuarea perpendiculara a punctului A trebuie să amâne AX segmentul“, egal cu AX segment. X „este numit un punct simetric punct în raport cu linia X g. În cazul în care X se află pe linia g, atunci este punctul simetric este foarte punctul de X. Evident, punctul simetric la punctul X“, există un punct X.

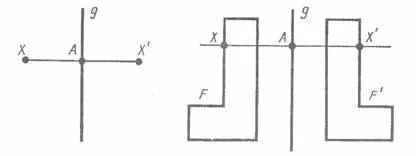
Cifrele de conversie în figura F F „în care fiecare punct X devine un punct X“, care este simetrică în raport cu o linie dată g, numită o transformare de simetrie în raport cu o linie dreaptă g. În acest caz, cifrele F și F „sunt numite simetric în raport cu o linie dreaptă g.

Dacă transformare de simetrie g ia o figura F relativ drept în sine, această cifră se numește simetrică în raport cu o linie dreaptă g, și o linie dreaptă g se numește axa de simetrie a figurii.

De exemplu, liniile care trec prin punctul de intersecție al diagonalelor dreptunghiului paralel cu laturile sale, dreptunghi este axa de simetrie. Direct să se întindă pe diagonală romburi este axa sa de simetrie.

Teorema: Conversia de simetrie în raport cu o mișcare de linie dreaptă.

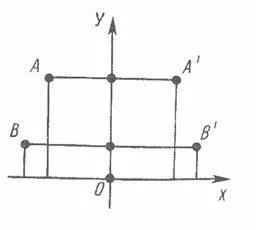
Dovada. Să luăm o anumită linie de axa y carteziene sistemului de coordonate. Lăsați un punct arbitrar A (x; y) F Figurine continuă la punctul A '(x', y ') figura F'. Din definiția de simetrie în raport cu un segment de linie care punctele A și A „egală cu ordonata și abscisa sunt diferite numai în semn: x“ = -x.

Ia două puncte arbitrare A (x; y) și B (x; y). Ei vor merge la punctul A '(-x, y) și B' (-x, y).

A'B'2 = - (x2 + x1) 2+ (y2-y1) 2

Acest lucru arată că AB = A'b“. Aceasta înseamnă că transformarea de simetrie în raport cu o linie dreaptă este o mișcare. Acest lucru dovedește teorema.

Simetria despre planul

Să o - orice plan fix. Din X cifre omit XA perpendicular pe planul unei continuate dincolo de punctul Aotkladyvaem AX segment“, egal cu XA. Punctul X „este numit un punct simetric în raport cu planul X a, și transformarea pe care o transformă într-un punct simetric X X“, se numește o transformare în raport cu planul de simetrie a.

În cazul în care X se află în planul unui, se presupune că X intră într-o. Dacă transformarea simetrie în raport cu un plan figură se traduce în sine, cifra este numit simetric față de un plan și un plan se spune planul de simetrie al figurii.

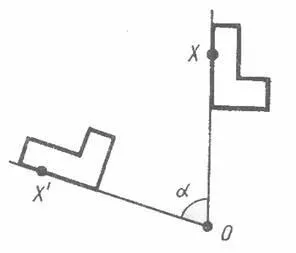
rotirea planului aproximativ un punct dat este o mișcare în care fiecare fascicul provine dintr-un punct rotit prin același unghi în aceeași direcție.

Acest lucru înseamnă că, dacă rotația în jurul punctului O este mutat la punctul X“, Bivolul și OX razele formează același unghi, indiferent de punctul X. Acest unghi se numește unghiul de rotație. Conversia forme prin rotirea planului numit, de asemenea, rândul său.

transfer paralel în spațiu

translație paralelă în spațiu este o transformare în care un punct arbitrar (x, y, z) se deplasează figura la un punct (x + a; y + b; z + c), în cazul în care numerele a, b, c sunt aceleași pentru toate puncte (x; y; z). spațiu schimburi paralel este dat de

exprimând coordonatele x „y“ punct, z“, în care punctul (x, y, z) cu translație paralelă. La fel ca și în planul următor proprietăți se dovedesc a fi transfer paralel:

1. transferul paralel de mișcare acolo.

2. Atunci când punctele de transfer paralele sunt deplasate în paralel (sau coincizând) Direct pe una și aceeași distanță.

3. Într-o deplasare paralelă în fiecare linie devine o linie paralelă la aceasta (sau în sine).

4. „există doar un transfer paralel, în cazul în care punctul A se muta la punctul A,“ Indiferent de punctele A și A.

Noul transfer paralel în spațiu este următoarea proprietate:

5. În deplasare paralelă în fiecare spațiu sau avion se mută în sine, sau în paralel cu planul său.

Intr-adevar, lasa un - un plan arbitrar, țineți avionul în două linii drepte care se intersectează a și b. În linii de transport paralele b și fie ei înșiși, fie în paralel linii drepte a „și b“ în mișcare. Un avion se mișcă într-un plan de „care se extinde printr-o directă“ și b“. Dacă planul unui „nu coincide cu, printr-o teoremă a două linii care se intersectează cu un plan paralel cu, respectiv, linii diferite plane care se intersectează, este paralelă cu, după cum este necesar.

Referințe:

1. Textbook actualizări 7-11 clase. AV Pogorelov

2. actualizări de manuale 10-11. AD Alexandrov.