Bernoulli

Nu vom vorbi de lung - va începe imediat cu definiția.

Schema Bernoulli - când n este realizată din experimente independente același tip, din care fiecare poate primi un eveniment de interes pentru noi A. și probabilitate cunoscută a acestui eveniment P (A) = p. Este necesar să se determine probabilitatea ca în timpul evenimentului A studiile n exact k apare din nou.

Problemele care sunt rezolvate prin schema Bernoulli, sunt extrem de diverse: de la simplu (cum ar fi „găsi probabilitatea ca trăgătorul a lovit un timp din 10“) la foarte severă (de exemplu, problema interesului sau cărți de joc). În realitate, acest sistem este adesea folosit pentru a rezolva problemele legate de controlul calității produselor și fiabilitatea o varietate de mecanisme, toate acestea vor fi cunoscute înainte de punerea în funcțiune.

Să ne întoarcem la definiția. Din moment ce vorbim despre studii independente, în fiecare experiment, probabilitatea evenimentului A este aceeași, doar două rezultate posibile:

A - apariție a unui eveniment A cu probabilitate p;
„Nu A“ - evenimentul A nu se pare că are loc cu probabilitatea q = 1 - p.

Cea mai importantă condiție, fără de care sistemul Bernoulli își pierde sensul - această constanță. Nu contează cât de multe experimente care nu am realizat, suntem interesați în același eveniment A. care are loc cu aceeași probabilitate p.

De altfel, nu toate problemele din teoria probabilităților sunt reduse la condiții constante. Acest lucru vă va spune orice profesor competent în matematici superioare. Chiar și un astfel de lucru destul de simplu ca a scoate bilele colorate de pe cutie, nu experiența cu condiții constante. Au luat o altă minge - raportul de culori în caseta sa schimbat. Prin urmare, ne-am schimbat și probabilitate.

În cazul în care condițiile sunt constante, este posibil să se determine cu exactitate probabilitatea ca un eveniment A apare exact k ori din n posibil. Să formuleze acest fapt ca o teorema:

Teorema lui Bernoulli. Să probabilitatea de apariție a evenimentului A în fiecare studiu este constantă și egală cu p. Apoi, probabilitatea ca studiile independente n evenimentului A apare exact k ori, se calculează după cum urmează:

unde C n k - numărul de combinații, q = 1 - p.

Această formulă se numește: formula Bernoulli. Este interesant de notat faptul că sarcinile enumerate mai jos, se rezolvă fără utilizarea acestei formule. De exemplu, putem aplica formula adăugarea de probabilități. Cu toate acestea, valoarea de calcul este pur și simplu nerealist.

Sarcină. Eliberați probabilitatea de produse defecte pe masina este de 0,2. Se determină probabilitatea ca o cursă de zece emise pe această mașină exact k piese sunt fără căsătorie. Pentru a rezolva problema pentru k = 0, 1, 10.

Prin ipoteză, suntem interesați în cazul O eliberare a produselor fără căsătorie, ceea ce se întâmplă de fiecare dată cu probabilitatea p = 1-0.2 = 0,8. Este necesar să se determine probabilitatea ca un eveniment va avea loc k ori. Evenimentul A este în contrast cu evenimentul „nu este o», adică problema produselor defecte.

Astfel, avem: n = 10; p = 0,8; q = 0,2.

Deci, găsiți probabilitatea ca toate piesele defecte (k = 0), adică doar o singură bucată, fără căsătorie (k = 1), și că piesele defecte nu la toate (k = 10), în joc:

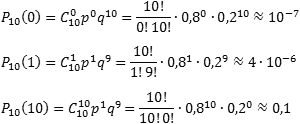
Sarcină. Monede arunca de 6 ori. De capete și cozi cu probabilitate egală. Găsiți probabilitatea ca:

stema va cădea de trei ori;
stema va cădea o dată;
stema va scădea cel puțin de două ori.

Deci, suntem interesați în cazul când A. creasta cade. Probabilitatea acestui eveniment este p = 0,5. Un eveniment de eveniment în contrast „, nu A», atunci când cade cozi care apare cu probabilitatea q = 1 - 0,5 = 0,5. Este necesar să se determine probabilitatea ca stema va scadea k ori.

Astfel, avem: n = 6; p = 0,5; q = 0,5.

Se determină probabilitatea ca stema a scăzut de trei ori, și anume, k = 3:

Acum definim probabilitatea ca haina a scăzut doar o singură dată, și anume, k = 1:

Rămâne să se determine cât de probabil stema se încadrează cel puțin de două ori. Principala dificultate - în expresia „cel puțin“. Se pare că vom aranja orice k. cu excepția 0 și 1, adică suma necesară pentru a găsi valoarea X = P 6 (2) + P 6 (3) +. + P 6 (6).

Rețineți că această sumă este de asemenea egală cu (1 - P 6 (0) - P 6 (1)), adică destul de toate opțiunile posibile „tăiat“ cele în care stema a scăzut de 1 ori (k = 1), sau nu a scăzut deloc (k = 0). Deoarece P 6 (1) știm deja, este necesar să se găsească P 6 (0):

Sarcină. Probabilitatea ca televizorul a ascuns defecte este 0.2. La depozitul a primit 20 de televizoare. Care este probabilitatea unui eveniment: că, în acest joc există două televizoare cu defecte ascunse sau trei?

Eveniment de interes A - prezența unui defect latent. Total N = 20 televizoare, latentă probabilitate defect p = 0,2. Prin urmare, probabilitatea de a primi TV fără defect latent este q = 1-0.2 = 0,8.

Obținem condițiile de pornire pentru schema Bernoulli: n = 20; p = 0,2; q = 0,8.

Să ne găsim probabilitatea de a obține două „defect“, televizorul (k = 2) și trei (k = 3):

Evident, P 20 (3)> P 20 (2), adică probabilitatea de a avea trei televizoare cu defecte ascunse mai multe sanse de a primi doar două dintre televizor. Mai mult decât atât, diferența nu este slab.

O mică notă despre factorialele. Mulți oameni au un vag sentiment de disconfort atunci când văd mențiunea „0“ (a se citi „zero factorial“). Deci, 0! = 1 prin definiție.

P. S. Dar cea mai mare probabilitate în ultima sarcină - este de a obtine patru televizorului cu defecte ascunse. - matematică și asigurați-vă că.

Pregătirea gratuită pentru examenul de 7 lecții simple, dar foarte util + teme pentru acasă