Având în vedere numărul de distribuție a unei probabilități variabile aleatoare discrete pentru a găsi lipsesc și pentru a construi

Aleatoare variabila X are doar patru valori: -4, -3, 1 și 2. Fiecare dintre aceste valori este nevoie de o anumită rată. Având în vedere că suma tuturor probabilităților trebuie să fie egală cu 1, atunci probabilitatea lipsește:

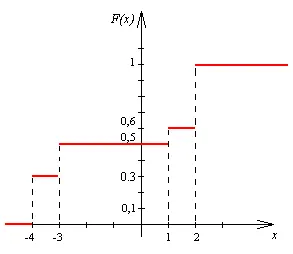
Formăm funcția de distribuție a variabilei aleatoare X. Este cunoscut faptul că funcția de distribuție, atunci:

atunci când, din moment ce nici o valoare a lui x (-4, -3, 1 și 2) nu sunt mai mici decât x. aceasta înseamnă;

atunci când, din moment ce numai valoarea -4 va fi mai mică de x. și evenimentul x = 1 apare cu o probabilitate egală cu 0,3, adică;

când, valori mai mici decât x. va fi X = -4 și X = -3, iar variabila aleatoare X poate lua prima sau a doua valoare, atunci;

Așteptarea unei variabile aleatoare discrete este suma produselor de valori ale variabilei aleatoare corespunzătoare probabilității, adică,

O dispersie de variabile aleatoare discrete găsi formula:

elemente de combinatorică

Numărul de combinații - - este numărul de moduri în care puteți selecta k elemente distincte ale elementelor n existente, fără a lua în considerare procedura de eșantionare.

Numărul de destinații de plasare - - este numărul de moduri în care puteți selecta k elemente distincte ale elementelor n existente, luând în considerare procedura de eșantionare.

Numărul de permutări - - este numărul de moduri în care puteți selecta n diferite elemente ale elementelor n existente, luând în considerare procedura de eșantionare.

Aici: - factorial

Acțiuni cu privire la evenimente

Eveniment - este doar un fapt care poate sau nu poate să apară ca rezultat al experienței.

Combinând evenimente A și B - este un eveniment care S. este aspectul sau un eveniment sau un eveniment B. A sau ambele evenimente în același timp.

Intersecția evenimentelor A și B - este un eveniment care S. este apariția simultană a ambelor evenimente.

O negare a evenimentului - acesta este un eveniment care nu este apariția evenimentului A. Desemnarea :.

Definiția clasică a probabilității

Probabilitatea evenimentului A - raportul dintre numărul de experimente. să conducă la apariția evenimentului A la numărul total de experimente:

Probabilitatea de multiplicare Formula

Probabilitatea evenimentului poate fi găsit de formula:

- probabilitatea evenimentului A,

- Probabilitatea evenimentului,

- Probabilitatea unui eveniment, cu condiția ca evenimentul A a avut loc deja.

Dacă evenimentele A și B - sunt independente (aspectul nu afectează aspectul celuilalt), atunci probabilitatea evenimentului este:

Formula plus Probability

Probabilitatea evenimentului poate fi găsit de formula:

- probabilitatea evenimentului A,

- Probabilitatea evenimentului,

- probabilitatea co-apariție a evenimentelor A și B.

Dacă evenimentele A și B - se exclud reciproc (nu pot apărea în același timp), atunci probabilitatea evenimentului este:

Formula totală probabilitate

Lăsați evenimentul A poate avea loc în același timp, unul dintre evenimentele ... - să le numim ipoteze. De asemenea, cunoscut - probabilitatea de a îndeplini ipoteze i-lea și - probabilitatea unui eveniment A, atunci când ipoteza i-lea. Apoi, probabilitatea unui eveniment A poate fi găsit de formula:

schema Bernoulli

Lăsați firul n studiile independente. Probabilitatea de apariție (de succes) a unui eveniment A în fiecare dintre ele este constantă și egală cu p. probabilitatea de eșec (adică fără apariție a evenimentului A) q = 1 - p. Apoi, probabilitatea de succese k in n studiile pot fi găsite prin formula Bernoulli:

Numărul cel mai probabil de succese într-o schemă Bernoulli - este numărul de apariții ale unui eveniment care corespunde cea mai mare probabilitate. Poate fi găsit de formula:

variabile aleatoare

(De exemplu, numărul de fete în familie cu 5 copii) (de exemplu, timpul de funcționare corespunzătoare a fierbătorului)

Caracteristici numerice ale variabilelor aleatoare discrete

Să o valoare discretă set de distribuție următoare: