aplicații geometrice ale Integrale curbilinii
Suprafața regiunii delimitate de curba închisă;
Volumul corpului format prin rotirea curbei închise în jurul unei axe.
Să \ (C \) este o curbă lină, continua pe portiuni care este descris de către vectorul \ (\ mathbf \ stânga (t \ dreapta), \, \ alpha \ le t \ le \ beta. \) Din lungimea curbei este exprimată prin următoarea linie integrală \ [> = >>> \ stânga (t \ dreapta)> \ dreapta | dt >> = >>> \ dreapta)> ^ 2> + >>> \ dreapta)> ^ 2> + >>> \ dreapta) > ^ 2 >> dt>,> \] unde \ (\ mare \ frac >>> \ normalsize \) - derivat și \ (x \ stânga (t \ dreapta), y \ stânga (t \ dreapta), z \ stânga (t \ dreapta) \) - componente vectorială \ (\ mathbf \ stânga (t \ dreapta) \).
Dacă curba \ (C \) este definită într-un plan, atunci lungimea sa este dată de \ [> = >>> \ stânga (t \ dreapta)> \ dreapta | dt >> = >>> \ dreapta)> ^ 2> +> >> \ dreapta)> ^ 2 >> dt>.> \] Dacă curba \ (C \) este un grafic prestabilit explicit, continuă și diferențiabilă funcția \ (y = f \ stânga (x \ dreapta) \) în planul \ (Oxy, \) atunci lungimea unei astfel de curbă este calculată cu formula \ [L = \ int \ limits_a ^ b >>> \ dreapta)> ^ 2 >> dx>. \] în cele din urmă, în cazul în care curba \ (C \) este dată în polar coordonate de ecuația \ (r = r \ stânga (\ theta \ dreapta), \, \ alpha \ le \ theta \ le \ beta, \) și funcția \ (r \ stânga (\ theta \ dreapta) \) este continuă și diferențiabilă în intervalul \ (\ stânga [\ dreapta] \), atunci lungimea curbei este determinată de expresia \ [L = \ int \ limits_ \ alpha ^ \ beta >>> \ dreapta)> ^ 2> +> d \ theta>. \]
Suprafața regiunii delimitate de curba închisă
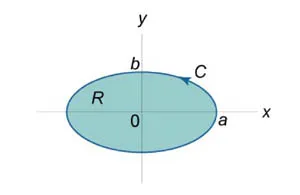
Să \ (C \) este o continua pe portiuni, curba netedă, închisă definită într-un plan \ (Oxy \) (Figura \ (1 \)). Apoi zona regiunii \ (R, \) limitată a curbei definită de formula \ [= -. \ Oint \ limits_C> = \ int \ limits_C> \] Se presupune aici că curba de bypass \ (C \) se face în sens antiorar.
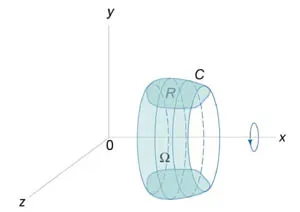
Volumul corpului format prin rotirea unei curbe închise în raport cu axa Ox
Să presupunem că zona \ (R \), situată în jumătatea superioară \ (y \ ge 0 \) și delimitate de o, continuă și închisă pe porțiuni curbe \ netede (C, \) care bypass-ul invers acelor de ceasornic. Ca rezultat, regiunea de rotație \ (R \) în jurul \ axei (Ox \) este format corpul \ (\ Omega \) (Figura \ (2 \)). Volumul corpului este determinat prin formulele \ [dx = >> <- 2\pi \oint\limits_C> = <- \frac\oint\limits_C dx> .> \]
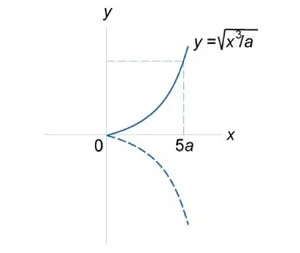
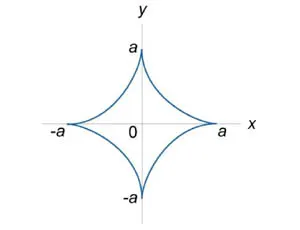
Găsiți lungimea curbei \ (a = \) furnizat \ (0 \ le x \ le 5a, \ y \ ge 0. \)
Găsiți lungimea unei curbe spațiu definit ca parametrically \ (\ mathbf \ stânga (t \ dreapta) = \ stânga (2> \ dreapta) \) unde \ (0 \ le t \ le 1. \)
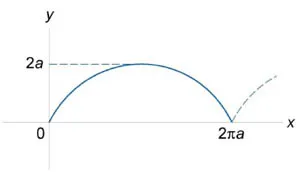
Găsiți lungime cicloidale definit parametrically vector \ (\ mathbf \ stânga (t \ dreapta) = \ stânga (\ dreapta), o \ stânga (\ dreapta)> \ dreapta) \) în intervalul \ (0 \ le t \ le 2 \ pi \) (Figura \ (5 \)).
Găsiți zona regiunii delimitate de o hiperbolă \ (y = \ mare \ frac \ normalsize, \) axa \ (Ox \) și verticale linii \ (x = 1, \) \ (x = 2 \) (Figura \ (7 \) ).
Calculăm zona folosind linia integrală. \ [> = <- \int\limits_ - \int\limits_ - \int\limits_ - \int\limits_ .> \] Găsim separat fiecare dintre integralele. \ [- \ int \ limits_ = - \ int \ limits_1 ^ 2 = 0, \] \ [- \ int \ limits_ = - \ int \ limits_0 ^ 0 = 0, \] \ [= - \ int \ limits_2 ^ 1 >>> = \ dreapta)> \ dreapta | _2 ^ 1> = <- \ln 1 + \ln 2 = \ln 2,> \] \ [- \ int \ limits_ = - \ int \ limits_0 ^ 0 = 0 \] Prin urmare, zona predeterminată este o zonă \ [S = \ ln 2. \]
Găsiți zona unei regiuni delimitată de o elipsă specificat parametrically ca \ (x = o \ cos t, \; y = b \ păcatul t, \; 0 \ le t \ le 2 \ pi \) (Figura \ (8 \)) .