3-9 de cotitură în jurul unei axe arbitrare în spațiu
3-9 se rotesc în jurul unei axe arbitrare în spațiu
Generalizat rândul său, cazul în jurul unei axe arbitrare în spațiu este comun, cum ar fi robotica, animație, modelare. Urmând logica discuției anterioare, rotația în jurul unei axe arbitrare în spațiu se realizează cu ajutorul unui transport simplu și rotație în jurul axelor de coordonate. Deoarece rotația în jurul axei de coordonate metoda este cunoscută, ideea de bază este de a combina o axă arbitrară de rotație cu una dintre axele de coordonate.
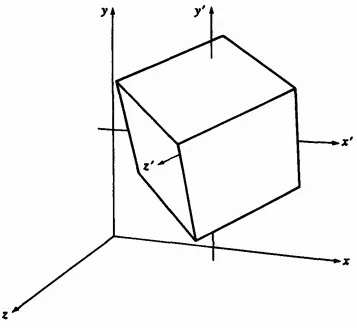
Fig. 3-6 câteva ture cu privire la sistemul local de coordonate.
Să presupunem că o axă arbitrară în spațiu trece printr-un vector direcțional. Rotație în jurul acestei axe printr-un anumit unghi, conform regulii de mai jos:
- efectua prin transfer, astfel încât punctul este la sistemul de origine;
- efectua rotații adecvate, astfel încât axa de rotație coincide cu axa;
- să se rotească cu un unghi față de axa;
- efectua o transformare inversă celei lăsate să se combine cu axa axei de rotație;
- executa retransfer.
In general, o axă arbitrară care trece prin origine coincide cu una dintre axele de coordonate, este necesar să se facă două pivotarea succesive despre celelalte doua axe. Pentru combinarea unei axe de rotație arbitrară cu axa de rotație a primei efectuate în jurul unei axe și apoi în jurul axei. Pentru a determina unghiul de rotație în jurul axei, folosită pentru traducerea unei axe arbitrare într-un plan pentru a proiecta primul ghid planul versorul axa (Fig. W3.7A). Componente și vector proiectat egale - și vector direcția componente montaj unitate a axei de rotație.
Fig. W3.7A, rezultă că
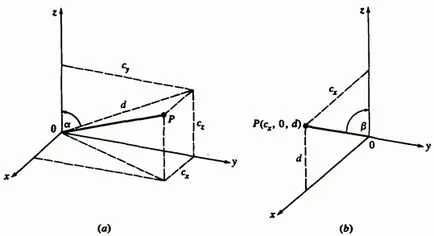
Fig. 3-7 se transformă necesare pentru alinierea cu versorul axei. (A) Rotația în jurul; (B) se întoarce.
După traducerea în planul prin rotirea în jurul axei, componenta vectorului unitate este egală, și egală componente, adică, vector direcție -component, așa cum se arată în Fig. 3-7b. Lungimea versorul este, desigur, 1. Astfel, unghiul de rotație în jurul axei dorită pentru combinarea unei axe arbitrare cu o axă egală
Apoi transformare completă poate fi scrisă ca
în care matricea de transport este
rotatie in jurul axei matricei de transformare
Și, în sfârșit, o rotație în jurul unei axe de rotație arbitrară este dată de matricea în jurul unei axe
În practică, unghiurile, și nu sunt calculate în mod explicit. Elementele matricei de rotație și (3-21) se obțin din ecuațiile (3-18) - (3-20) prin efectuarea a două operațiuni de divizare și rădăcină pătrată. Cu toate că aceste rezultate au fost dezvoltate pentru o axă arbitrară în primul cadran, acestea sunt aplicabile în toate cadranele.
În cazul în care componentele vectorului direcția unei axe necunoscute arbitrar, atunci, cunoscând al doilea punct de pe axa, ele pot determina prin normalizarea vectorului care leagă primul și al doilea termen. Mai precis, axa unui vector egal
Normalizarea furnizează componentele vectorului:
Mai complet această metodă este ilustrată în exemplul următor.
Exemplul 3-10 Rotirea în jurul unei axe arbitrare
Să considerăm un cub cu un unghi de trunchiat prezentat în Fig. 3-8a. Coordonata vectori nodurile sunt
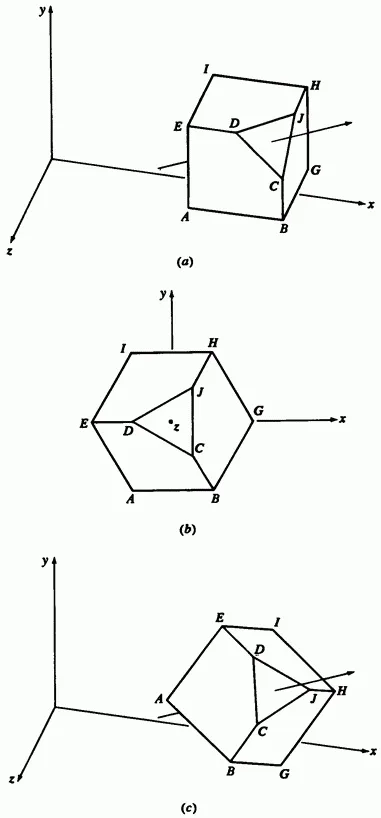
Fig. 3-8 Rotație în jurul unei axe arbitrare.
Cube trebuie să fie transformat în jurul unei axe care trece prin punctul și colțul opus pe diagonală. Axa este dirijată din punct la colțul opus și trece prin centrul marginii colț.
Mai întâi vom defini o unitate de componente vectoriale ale axei de ghidare de rotație. Având în vedere că un unghi de tăiere triunghi se află, de asemenea, pe axa, rezultă din (3-26), care
ecuațiile folosind (3-18) - (3-20) obținem
Deoarece punctul se află pe axa de rotație a matricei de transfer este
Apoi, matricea de rotație, care combină o axă arbitrară de rotație a axei, sunt de forma:
matrice Inverse și se obțin prin înlocuirea valorilor pentru unghiurile și, respectiv, în ecuația (3-22) - (3-24).
Coordonatele transformate sunt intermediari
Acest rezultat intermediar este ilustrat în Fig. 3-8b. Rețineți că punctul este egal.
Rotație în jurul unei axe arbitrare este acum echivalent cu o rotație în jurul unei axe. În consecință (a se vedea. (3-7)),
Obiectul transformat este returnat în locația sa „original“ în spațiul folosind transformarea
Acest rezultat poate fi obținut fie prin contactarea și combinarea matricile constitutivă sau tratarea matricei în sine. Notă, întâmplător, care reprezintă doar rotații. stânga sus este o transpunere exactă -submatrix superioară submatricile din stânga.
coordonatele rezultate sunt
Fig. 3-8C arată obiectul convertit.