1_Prakt_excel ZLP
Numărul de lucru practice 6. Exemplu de EXCEL pentru rezolvarea problemelor de programare liniară.
Obiectiv: Pentru a învăța să formaliza provocările economice, pentru a construi modele matematice pentru a găsi și interpretarea rezultatelor.
Astfel de probleme sunt rezolvate în Excel folosind Solver.
În cazul în care un model matematic al procesului în curs de investigare și restricțiile privind valorile parametrilor săi sunt liniare, atunci sarcina este de a realiza o problemă de programare liniară.
Soluții instrument de căutare pot fi folosite pentru sarcini care includ multe izmenyaemyhyacheek și ajută să găsească o combinație de variabile care stabilesc celula țintă la valoarea dorită (de exemplu, maxime sau minime). De asemenea, vă permite să specificați una sau mai multe constrângeri - condiții care trebuie îndeplinite în căutarea de soluții.
Exemple de probleme care pot fi rezolvate prin intermediul unor soluții de căutare:
problema de atribuire,
elaborarea unui plan optim de producție,
decizia ecuației de regresie.
Înainte de a contacta căutarea instrumentului pentru o soluție. aveți nevoie pentru a analiza problema și de a construi un model matematic. Pentru a construi modelul ar trebui:
a) determina ce variabile ale modelului;
b) selectați funcția țintă;
Limitele c) stabilite să fie îndeplinite de variabile.
Atunci când pregătește o foaie de lucru pentru a rezolva problema trebuie să:
ia o serie de celule pentru stocarea variabilelor;
într-o singură celulă pentru a intra în funcția obiectiv. Funcția obiectiv este întotdeauna dependentă de variabile, astfel încât într-o celulă cu o funcție obiectiv de a fi trimiteri la celula, unde sunt stocate variabilele;
pregătesc valori și formule pentru specificarea constrângerilor. Din moment ce limitări sunt impuse variabilele din formulele pentru specificarea restricțiilor de a fi trimiteri la celula în care sunt stocate variabile.
Soluțiile de dialog oknaPoisk
După construirea unui model matematic se poate referi la mijloacele de a găsi soluții. Pentru a face acest lucru, utilizați instrumentele de comandă - Solver. (. Figura 1) - (Dacă această opțiune nu este disponibilă, trebuie să efectuați mai întâi următorii pași :. Call-in-uri caseta de dialog din comanda Instrumente Add-Ins și verificați soluția de căutare caseta) caseta de dialog Solver apare.
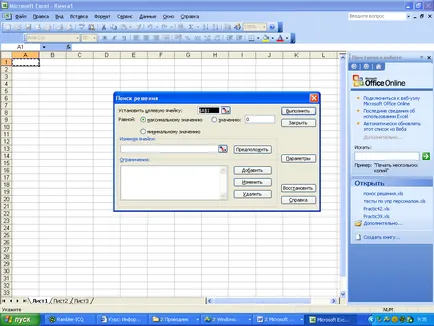
Fig.1 Window Solver.
În obiectivul Set pentru a avea o legătură într-o celulă cu o funcție de țintă. Dacă înainte de a apela Solver instrument selectați celula cu funcția obiectiv (recomandat), atunci acest câmp va fi deja completat.
Mai jos sunt controalele - comutatoare, - Specifică valoarea funcției obiectiv care urmează să fie realizate în rezolvarea problemei: minim, maxim, sau o anumită valoare specifică.
Prin varierea câmp vă permite să specificați un interval de celule în care sunt situate necunoscutele, afectează funcția obiectiv.
Lista limitărilor este toate restricțiile impuse de starea butonul Add. O casetă de dialog va apărea (Fig. 2).

Ris.2.Okno dialog pentru a stabili restricții
Butonul Add permite setarea unor limitări, butonul OK adaugă constrângerea și închide fereastra.
Butonul Edit din caseta de dialog vă permite să căutați o soluție pentru a modifica selectat în lista limitărilor. În acest caz, ecranul va afișa o casetă de dialog Adăugarea restricție (Fig. 2), controalele deja completate.
Butonul Delete din caseta de dialog vă permite să căutați o soluție pentru a elimina constrângerea selectată. Odată ce toate datele pentru instrumentul Solver va fi setat, utilizați butonul Run. Dacă se găsește o soluție, Excel va da acest mesaj, iar rezultatele calculelor sarcinii vor fi plasate în celulele corespunzătoare. Dacă o soluție nu poate fi găsită, Excel va emite, de asemenea, acest mesaj.
Soluții Opțiuni de căutare
Pentru a modifica setările pentru a găsi o soluție a problemei, trebuie să utilizați butonul de dialog Opțiuni de căutare caseta de soluție (fig. 1) pentru a afișa caseta de dialog soluții avansate de căutare (Fig. 3).
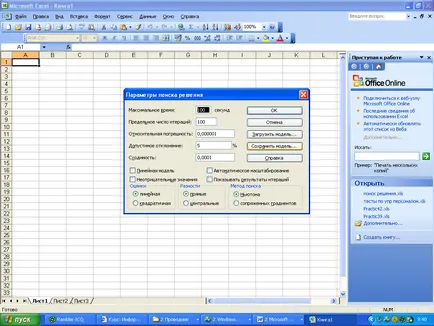
Fig. 3.Zadanie parametrii poiskaresheniya
Tabel. 1. o descriere a elementelor acestei ferestre. Trebuie remarcat faptul că valorile și controalele de stat, valorile implicite sunt de obicei suficiente pentru cele mai multe scopuri.
Tabelul de căutare soluții 1.Parametry
Introduceți datele sursă și formulele din foaia de calcul, așa cum este indicat mai jos:
activa, faceți clic pe Solver din meniul Instrumente și să descrie parametrii săi, după cum se arată mai jos:
Nu uitați să indicați în setările de pe modelul liniar.
Lansați căutarea unei soluții. Dacă ați făcut totul corect, atunci soluția va fi la fel ca în Fig. 6:
Din decizia arată că planul de eliberare optimă prevede producția de 80 kg de dulciuri, „B“ și 200 kg de dulciuri „C“. Candy „A“ nu este în valoare producătoare. S-a obținut prin tine profit de 4000 p.
Obiectivul dieta 2. Elaborarea
O mică întreprindere agricolă produce rațe de îngrășare.
În același timp, există o oportunitate reală de a utiliza două tipuri de furaje - și Korm1 Korm2.
Costul de 1 kg: Korma1 - 0,8 ruble. și Korma2 - 1 freca.
Fiecare alimente în compoziția sa conține vitale pentru păsările nutrimente B1, B2 și B3, dar în proporții diferite. Aceste proporții se arată în Tabelul 14.
Cantitatea de nutrienți în unități de 1 kg de furaj:
9 unități de nutrienți B1
8 B2 Substanțe și unități
B3 12 unități de substanță.
Este necesar pentru a face un minim de rație costul zilnic de păsări de curte constând din Korma1 și Korma2, ci să stabilească condiții cu privire la conținutul de nutrienți în ea au fost îndeplinite.
Problema 3. Problema de transport
Regiunea are două fabrici și trei consumatori de produsele lor - fabrici de construcții casa. Tabelul arată Diurnele producției de ciment, nevoia de zi cu zi pentru ea combina si costurile de transport 1T de ciment de la fiecare plantă fiecare plantă.
Este necesar pentru a face un plan de trafic zilnic de ciment, în scopul de a minimiza costurile de transport.
Decizia cu cantități necunoscute sunt volumul traficului. Lăsați volumul xij- de transport de ciment de la fabrica de la J- lea j- plantelor lea, Pij - costul fabricii de ciment de transport 1T în J- lea j- plantelor lea. Apoi, funcția obiectiv este costurile totale de transport:
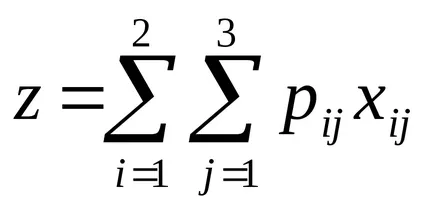
Necunoscut în această problemă trebuie să îndeplinească următoarele restricții:
Volumele de trafic nu poate fi negativă, adică, xij≥ 0.
Toate ciment cu plante care urmează să fie exportate. Să ai - volumul producției de ciment în uzina i-lea. Apoi, această restricție este după cum urmează:
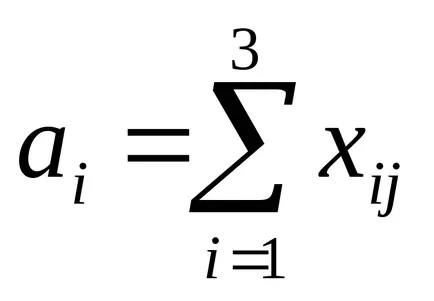
Nevoile tuturor instalațiilor din ciment trebuie să fie îndeplinite. În cazul în care pentru a indica bj cererea de ciment din plante j-lea, această condiție poate fi scrisă ca:
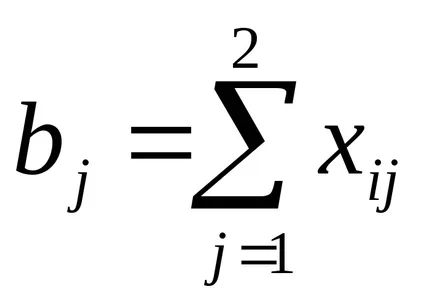
Datele de intrare pot fi aranjate în foaia de lucru așa cum este prezentat în Fig. 7. La prepararea acestor exemple au fost făcute setările pentru celulele din foaia de lucru formula afișată și nu valorile calculate cu ajutorul acestor funcții, care arată ce formule ar trebui să fie utilizate pentru a pune în aplicare funcția obiectiv și constrângerile. Pentru a rezolva problema, nu este necesar să se afișeze formula în locul valorilor. După pregătirea foii de lucru pe care doriți să apelați și să căutați o soluție pentru a umple caseta de dialog, așa cum este prezentat în Fig. 8. În plus, trebuie să utilizați butonul Opțiuni, apoi selectați caseta de validare Lineynayamodel.
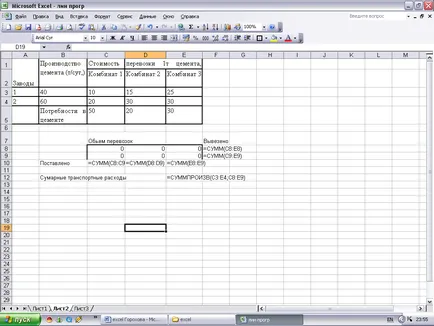
Fig. 7. Datele inițiale pentru problema transportului de ciment
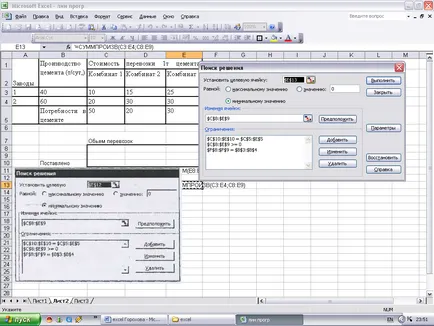
Figura 8. Stabilirea datelor inițiale pentru soluțiile caseta de căutare
După apăsarea instrumentul Run Solver găsește un plan optim pentru transportul zilnic de ciment.
Notă. În acest exemplu, problema este echilibrată: volumul total de producție este volumul total în care are nevoie. Prin urmare, în acest model, nu este necesar să se ia în considerare costurile asociate stocării (supraproducție) sau cu termen de livrare scurt (deficitul). În caz contrar, ar fi necesar să se introducă în model:
în cazul supraproducției - o plantă fictive, costul unitar de transport al produselor care va fi egală cu costul de depozitare și de necesitatea de produs - depozitarea volumului de producție excedentare în fabrici;
în cazul deficienței - o fabrică fictive, costul transportului de la care va fi egală cu costul amenzilor pentru eșecul de a furniza produse, ca volumele de trafic - volumele de aprovizionare scurte de produse în punctele de distribuție.
Planta produce carcasa pentru frigidere și le completează cu echipamentele furnizate de alte companii, fără restricții. Tabelul arată standardele de costurile forței de muncă, costul materialelor pentru fabricarea de cochilii pentru aceste resurse limitări pe lună și veniturile din vânzarea frigiderului fiecare dintre cele cinci mărci. Găsiți frigidere lunar foaie de parcurs, maximizarea profiturilor.
7. fabrica de ceai de ambalare produce note de ceai A și B, prin amestecarea trei ingrediente: ceai indian, Georgia și Krasnodar. Tabelul I prezintă ingrediente ale ratelor de aplicare, volumul stocurilor fiecărui ingredient și profit din vânzarea de 1 m ceaiuri A și B.
Rata de consum (t / zi)
Profit din tone de produse realizatsii1 (rub.)
Pentru a continua descărcarea aveți nevoie pentru a asambla o imagine: