zona unui poligon, programmirovanie-DLA-sshool
Lecția din seria „algoritmi“ geometrice
Bine ai venit, dragă cititor.
Rezolvarea multe probleme de geometrie computațională se bazează pe găsirea aria unui poligon. În această lecție, obținem o formulă pentru calcularea suprafeței poligonului a coordonatelor nodurilor sale, scrie funcția de calcul pătrat.
Sarcină. Se calculează aria unui poligon. având în vedere coordonatele nodurilor sale, pentru a le evita sensul acelor de ceasornic.
Informații de la geometrie computațională
Pentru a obține aria unui poligon, avem nevoie de informații din geometria computațională, și anume, zona orientată spre concept al triunghiului.
Zona Oriented triunghiului - aceasta este o zonă comună dotată cu un semn. Semnul zonei orientate triunghiului ABC este același cu cel al unghiului orientat între vectorii și. Asta este, semnul său depinde de ordinea de noduri de transfer.
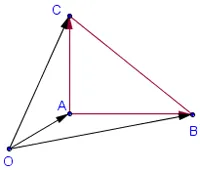
Fig. Dreptunghiular - 1 triunghi ABC. Suprafața sa este orientată (este mai mare decât zero, ca pereche este orientat pozitiv). Aceeași valoare poate fi calculată într-un alt mod.
Fie A - un punct arbitrar al avionului. În zona noastră de desen de triunghi se obține ABC în cazul în care aria triunghiului OBC zonele scădeți OAB și OCA. Astfel, pur și simplu adăugați în sus zonele de triunghiuri orientate OAB, OBC și OCA. Această regulă funcționează pentru orice alegere a punctului O.
În mod similar, pentru a calcula suprafața oricărui poligon să se plieze zone orientate de triunghiuri
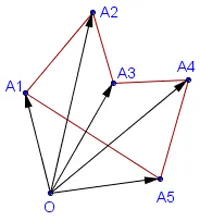
În concluzie, se transformă zona de poligon, luat cu semnul plus, în cazul în care stânga (ocolind de frontieră contra-sensul acelor de ceasornic), și cu semnul minus, dacă este să dreapta (runda sensul acelor de ceasornic), atunci când traversează poligon în pantă.
Astfel, calculul zonelor poligon redus pentru a găsi aria unui triunghi. Să vedem cum să-l exprime în coordonatele.
Produsul vectorial a doi vectori în plan este aria paralelogramului construit pe acești vectori.
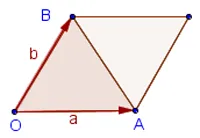
produs Vector, exprimat în termeni de coordonatele vectorilor:
zonă a unui triunghi este egală cu jumătate din acest domeniu:
Ca punct O, care este de a lua originea, atunci coordonatele vectorilor, pe care se calculează aria vizată, egală cu coordonatele punctelor.
Fie (x1 y1.), (X2 y2.), ..., (xN, in) - coordonatele vârfurilor poligonului în ordine sau sustrage sens antiorar. Apoi va fi orientată S este aria:
Aceasta este formula noastra este de lucru, este utilizat în programul nostru.
Dacă coordonatele nodurilor sunt specificate în traversal de sens anti-orar, numere S, calculate în conformitate cu această formulă, va fi pozitiv. În caz contrar, acesta va fi negativ, iar pentru zona geometrică de obicei am REQ-Dimo ia valoarea absolută.
Deci, ia în considerare programul pentru a găsi aria unui poligon definit prin coordonatele nodurilor.
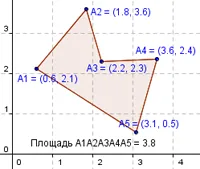
Vertex coordonate citește din fișierul input.pas. sunt stocate în matrice A sub formă de două câmp. Pentru comoditate, poligonului este introdus în traversal matrice n + 1 elemente, a căror valoare este egală cu primul element de matrice.
intrare:
5
2.1 1.8 3.6 0.6 2.2 2.3 3.6 2.4 3.1 0.5
Imprint:
S = 3,91
Ne vedem în lecția următoare.