vibrații șir de caractere
Scop: studiul fenomenelor val, condițiile de existență a undelor staționare, studiul proprietăților elastice ale șirului.
Principala poziție teoretică
Să punctul oscileze, se afla intr-un mediu în care sunt interconectate toate particulele. Apoi, energia de vibrație poate fi transmisă în jurul punctului de la puncte, declanșând modificări ale acestora. Fenomenul de propagare a vibrațiilor într-un mediu numit val. In aceasta oscilanta particulele nu se misca cu procesul oscilatorie omniprezentă, și fluctuează în jurul pozițiilor lor de echilibru.
În cazul în care un singur val distribuit în mod liber într-un mediu infinit, este numit o bandă de alergare. Noi formează ecuația unui undă care permite să se determine deplasarea de orice punct al valurilor în orice moment.
Fig. 9.1. Pentru a obține ecuația unui val de deplasare
Să considerăm un mediu omogen continuu
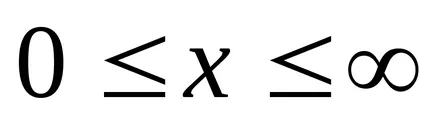

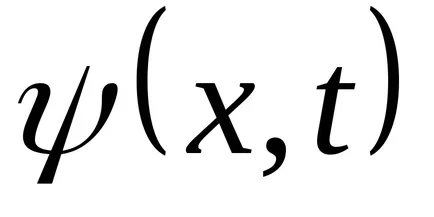
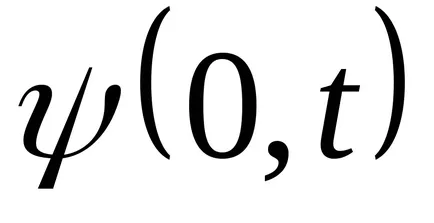


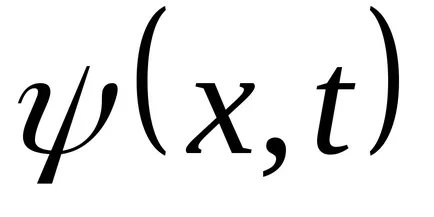
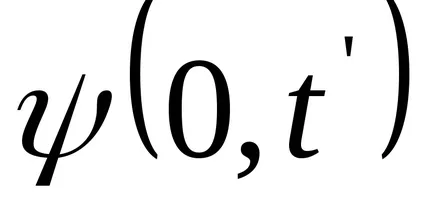


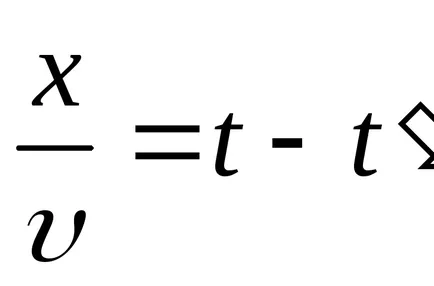
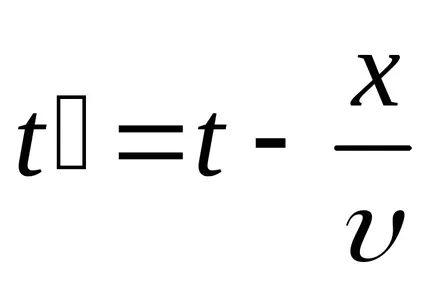
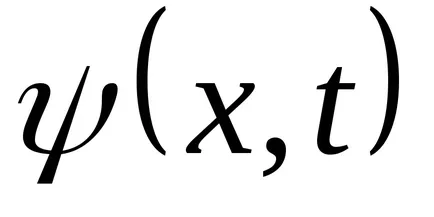
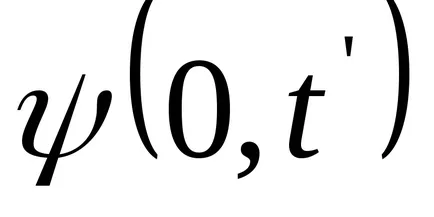

Funcția (9.1) Transform:
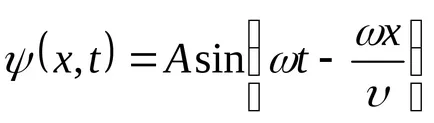
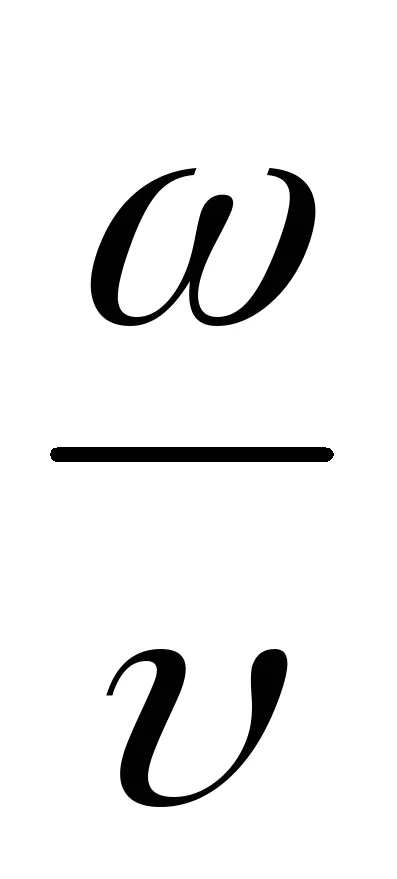
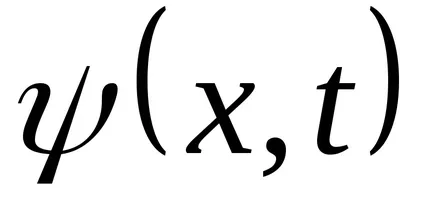
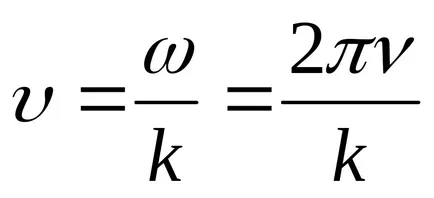


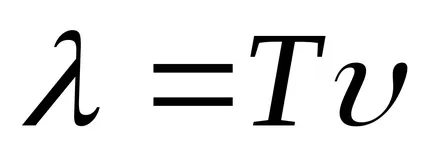
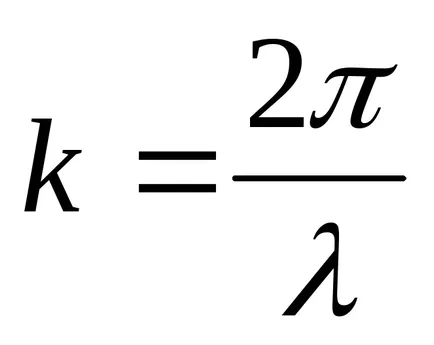
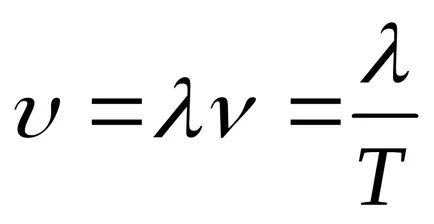
Ecuația (9.1) este ecuația undelor de deplasare tridimensional (sau plate). Pentru o anumită x este de a determina poziția punctului (coordonate poziției de echilibru x) la orice moment dat t. Pentru un anumit T permite determinarea poziției instantanee a punctelor oscilante.
Astfel, vedem că mișcarea valurilor deține dublă frecvență. Pe de o parte, fiecare particulă a mediului este supus mișcării periodice în timp, pe de altă parte, în fiecare moment, toate particulele sunt plasate pe linie, care forma se repetă periodic în spațiu.
Definim viteza de propagare a vibrațiilor longitudinale de-a lungul demon cursul unei tije lungi, cu o secțiune transversală constantă.
Fig. 9.2. Propagarea deformare elastică a lungul tijei
rideystvii pe partea stângă a forței

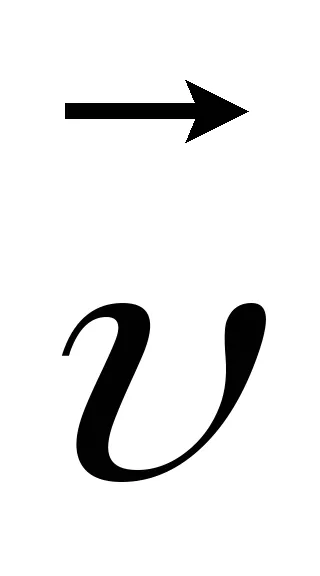
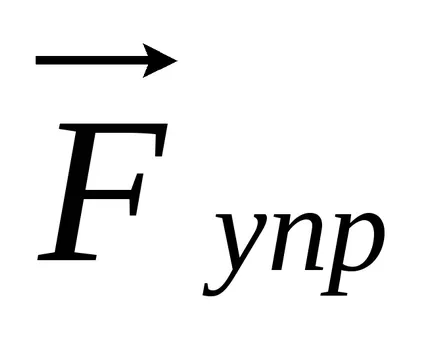
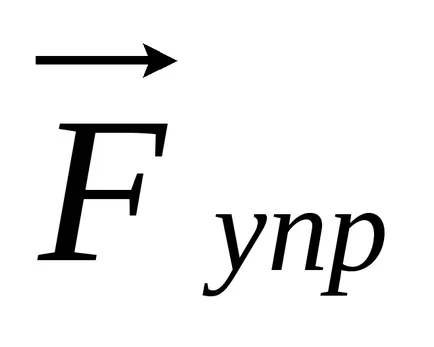

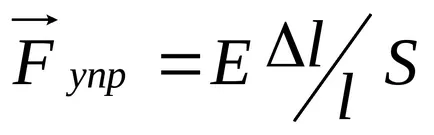

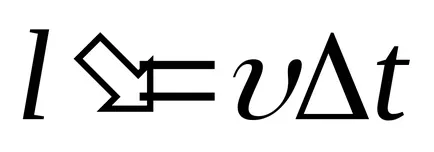
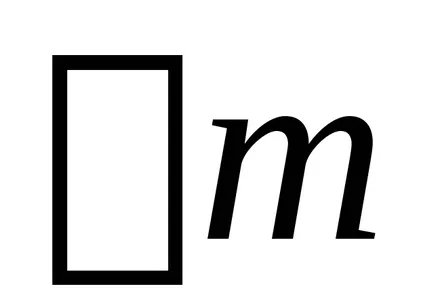
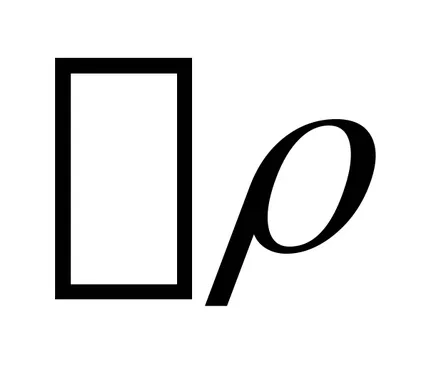
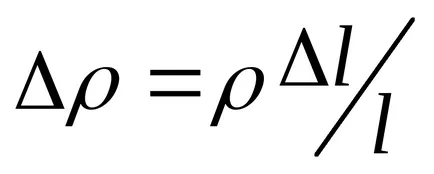
unde
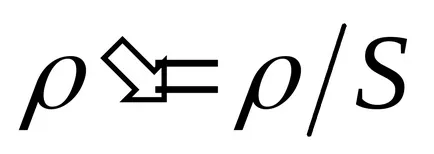
Ecuația (9.1) descrie un val de înmulțire în direcția pozitivă a axei Dl. Oh. La schimbarea direcției de propagare a undei la termenul opus al doilea în argumentul cosinusul schimbă semnul, ca

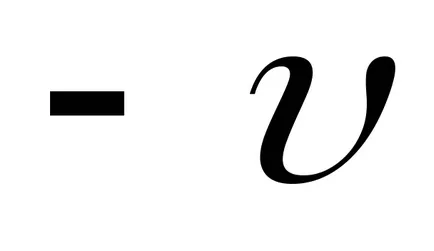
Luați în considerare acum propagarea undelor într-un șir de caractere fixat la ambele capete. În acest val, se deplasează într-o singură direcție, după ce a ajuns la al doilea capăt fix al șirului, și se va răspândi reflectat în direcția opusă. Astfel, de-a lungul lungimii undelor șir apar fenomene de suprapunere propagă în direcții opuse. Dacă proprietățile fluidului nu se schimbă sub efectul undei de înmulțire, principiul superpoziției se realizează, prin care fiecare val propagat în mediu independent de celelalte. În acest caz, z deplasarea rezultantă a particulelor de dimensiune medie este definită ca fiind cantitatea de z1 dislocare și z2. cauzată de trecerea undelor individuale. Ca urmare, aceasta va avea loc în diferite puncte ale câștigului mediu sau atenuării oscilații în funcție de faza de vin perturbație.
valuri de adiție, în care în puncte diferite ale mediului sunt formate de amplificare și de atenuare a amplitudinii oscilației este numită valuri de interferență. Acest model de interferență se menține în timp.
Luați în considerare interferența a două valuri de amplitudine egală călătoresc în direcții opuse, la fel ca în cazul unui șir de caractere fixat la ambele capete. Este necesar să se ia în considerare fenomenul următor. După reflecție de la capătul fix reflectat de deformare are semnul opus. Acest lucru este de înțeles atunci când consideră că, în deplasarea de capăt fixat tot timpul absent din punctul de fixare forțele care se opun șirul de intrare de îndoire. Aceste forțe generează o îndoire de semn opus, începe să se propage în direcția opusă. Prin urmare, deformarea în semn prejudecată reflectată este inversat. În cazul în care unda armonică reflectat, o astfel de modificare este echivalentă cu „pierderea“ jumătate de undă la reflecție.
Astfel, suprapunerea a două valuri dă următoarele:
.
Folosind diferența formulei sinus, obținem
Această expresie se numește ecuație de undă staționară, presupunând oscilații staționare, adică modul care se produce după valuri repetate rula între legăturile șir. De la (9.4) vedem că în mediul undei staționare toate punctele (orice valoare a lui x) variază cu sinuos frecvență unghiulară.
Amplitudinea oscilației este diferit pentru diferite puncte și este definit de (9.4), după cum urmează:
Din această din urmă expresie rezultă că există un punct al mediului, numite noduri, în care nu există fluctuații zm = 0, deci, z = 0. Coordonatele acestor puncte sunt determinate din condiția ca sinusul în (9,5), adică
Prin urmare, din moment
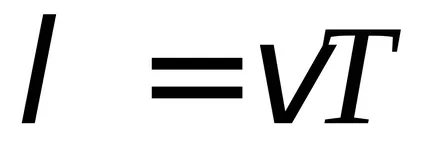
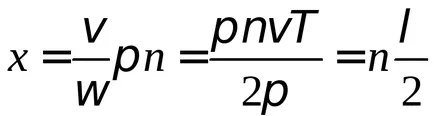
Prin urmare, distanța dintre noduri adiacente este egală cu jumătate din lungimea de undă. Deoarece nodurile în orice moment să rămână în repaus, valul în picioare nu este direcționat de transfer de energie, energia nu poate trece prin nodul. Transferul de energie de-a lungul șirului este doar o undă.
Aceste puncte la care valoarea amplitudinii atinge un maxim

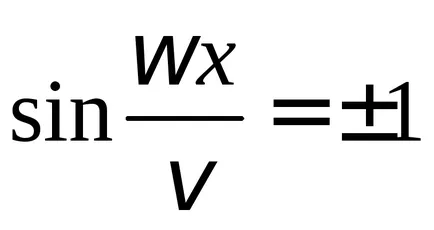
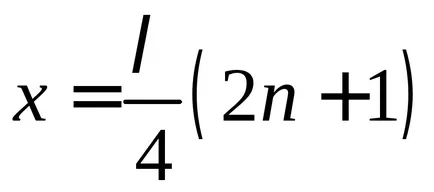
factor
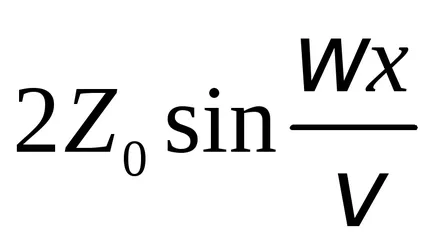
Astfel, se formează un undă staționară numai atunci când dimensiunea corectă șir raportul și lungimea de undă (frecvență de oscilație). Pentru diferite valori ale lui n = 1, 2, ... obținem diferite tipuri sau moduri de oscilații, în care n definește numărul de ventrele și nu noduri. De la (9.6) cu (9.7) obținem expresia pentru frecvențele la care undele staționare sunt stabilite în șirul
frecvențe
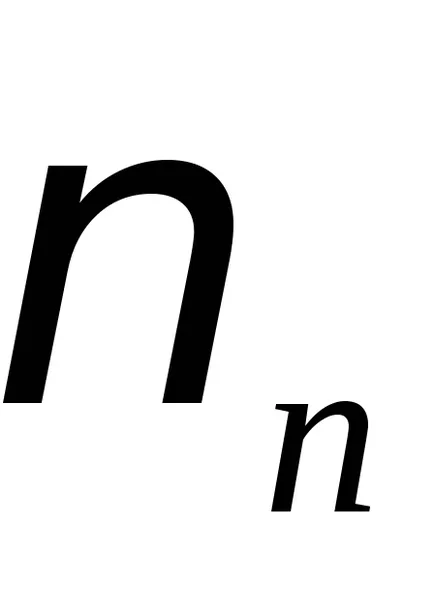
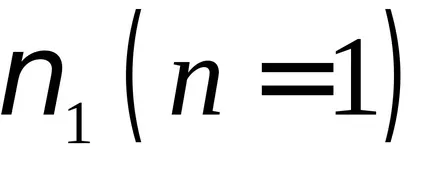
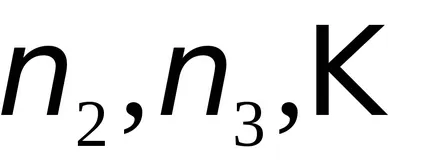
În general, în vibrațiile șir pot exista cu diferite frecvențe naturale. Astfel, împreună cu tonul fundamental n = 1, poate fi supratonuri excitat n = 2, 3, 4, ....
ecuațiile de mai sus obținute descriu mișcarea perfect șir flexibil în vid. În cazul în care vibrațiile șirul este întotdeauna o energie reală au loc pierderi.
O parte din energia se pierde din cauza frecării aerului, pe de altă parte trece prin capetele șirului, etc. Pentru a menține oscilații neamortizate este un vibrator. În cazul în care pierderea de energie în precizia este compensată de energia care vine din vibrator, șirul poate fi văzut valuri în picioare. Dar acum, șirul trebuie să fie transferul de energie. Prin urmare, valurile care călătoresc vor exista, împreună cu picioare, cu rezultatul că unele site-uri vor fi neclare. În cazul în care pierderile de energie pentru perioada sunt mici în comparație cu furnizarea de energie de vibrație în șirul, distorsiunea undei staționare de călătorie-val va fi nesemnificativ.
O altă abordare a teoriei de mai sus este eterogenitatea șir de neglijare. În șiruri reale și densitatea și tensiunea poate fi functiile continue ale coordonatelor X. De exemplu, dacă șirul este suspendat vertical, greutatea contului șir va conduce la faptul că tensiunea din părțile superioare este mai mare decât partea de jos. Orice inhomogeneity va conduce la o denaturare a formei de undă, deoarece oscilație sinusoidală în spațiul de doar o caracteristică a modurilor normale ale sistemelor omogene.