Vectori și matrici
Vectori și matrici.
Cu o secvență ordonată de numere a1 reale, a2, .... Puteți lega un vector de concept de asociat în spațiul n-dimensional și desemnat ca:
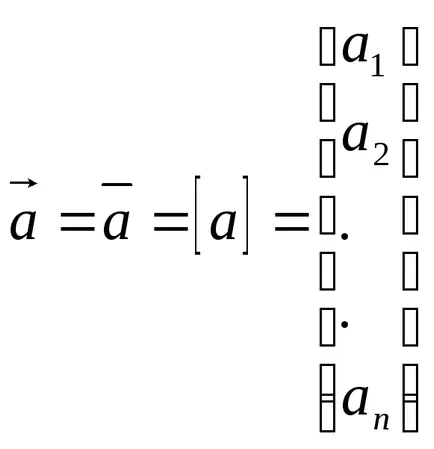
Tipuri și caracteristici ale vectorilor.
Zero vector - vector, toate ale cărei componente sunt zero.
Versorul - vector de lungime egală cu o:
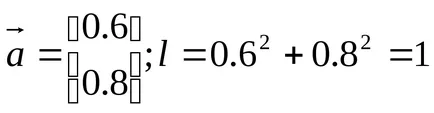
vector transpusa - un vector ale cărui componente sunt aranjate într-un rând:
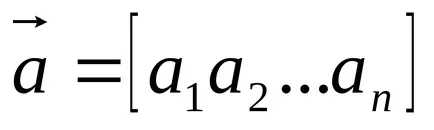
Doi vectori de aceeași dimensiune sunt egale, atunci când acestea sunt componentele respective:
Setul de numere aranjate într-o matrice dreptunghiular format din n rânduri și m coloane, numita matrice și se notează:
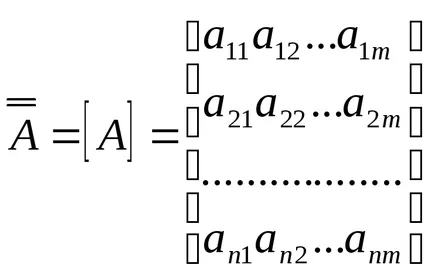
Poziția elementului

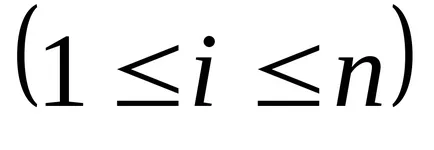
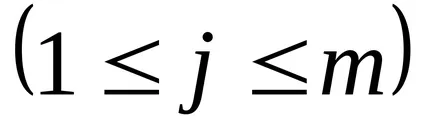
line Vector - matrice constând dintr-un singur rând n = 1
Vector Coloană - matrice constând dintr-o coloană de m = 1
O matrice pătrată - matrice în care n = m
triunghiular superior - matrice ale cărei
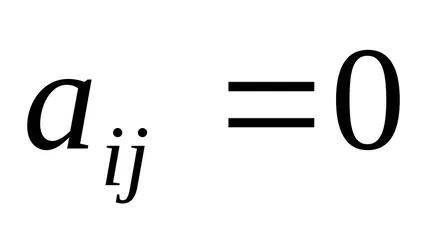
triunghiular inferior - matrice ale cărei
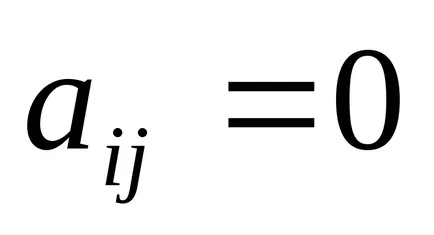
Diagonal - matrice a cărui
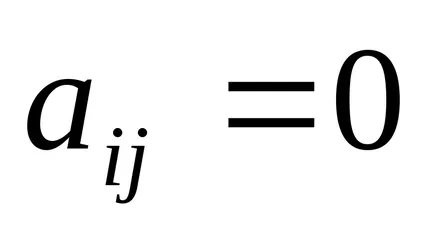
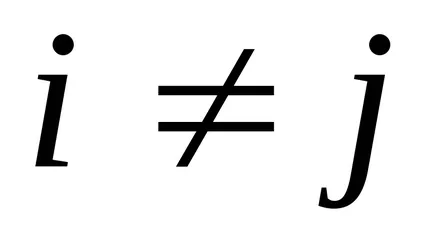
Identitatea - matrice ale cărei
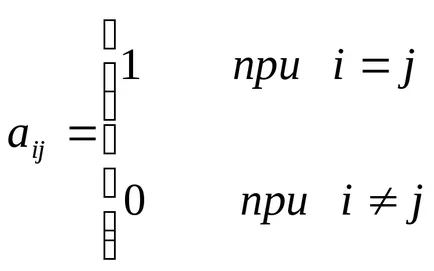
egalitatea de matrici
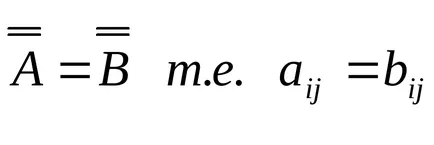
Caracteristici și funcționare.
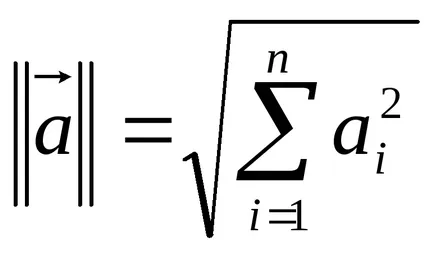
Norma matricei (euclidiană).
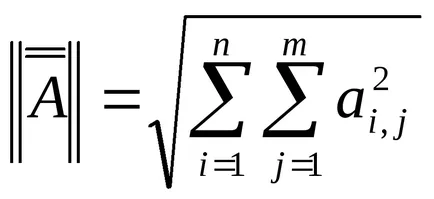
Adunare și scădere a vectorilor.
Adăugați și scade doar vectorul cu aceleași dimensiuni. Rezultatul adăugării (scădere) este un vector ale cărui componente sunt egale cu suma (diferența) dintre componentele respective ale altor doi vectori.
Adunare și scădere matricelor.
Adăugați și scade doar matricea cu aceeași dimensiune. Rezultatul adăugării (scădere) este o matrice ale cărei elemente sunt egale cu suma (diferența) a elementelor respective ale celorlalte două matrice.
Proprietatea adaosului (scădere) a matricelor:
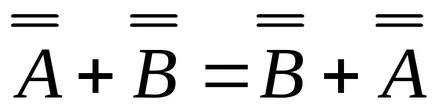
Multiplicarea unui vector printr-o constantă.
Rezultatul multiplicării este un vector ale cărui componente sunt egale cu produsul dintre componentele corespunzătoare ale vectorului de intrare printr-o constantă.
Multiplicarea unei matrice printr-o constantă.
Rezultatul multiplicării este o matrice ale cărei elemente sunt egale cu produsul elementelor respective ale matricei originale printr-o constantă.
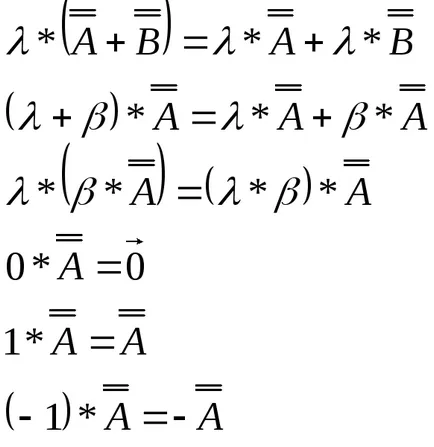
Transpune matrice - o înlocuire a rândurilor de coloane, adică,
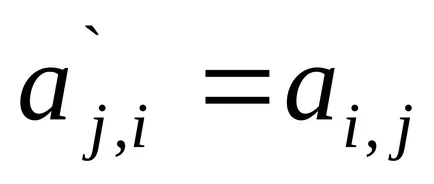
Numărul de coloane matricei A trebuie să fie egal cu numărul de rânduri ale matricei B.