unități de model de simulare calculat cistem regulament Mathcad automată - partea 2
Caracteristicile de frecvență logaritmice
În cele mai multe cazuri, caracteristicile de amplitudine și frecvență de fază reprezentată pe o scară logaritmică. Astfel de caracteristici de frecvență logaritmice sunt foarte convenabile pentru calcule inginerești.
În construcția caracteristicii logaritmice de frecvență amplitudine (LACHH) de-a lungul axei ordonatei reprezintă valoarea
Unitatea de măsură pentru care un decibel (dB). De-a lungul abscisei frecventa axa W pe o scară logaritmică (Figura 8).
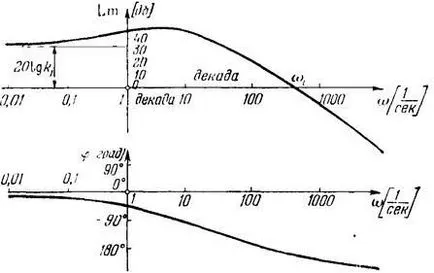
Figura 8. Caracteristicile de frecvență logaritmice.
Unitate de uniformă pe axa x este un deceniu - fiecare segment în care valoarea frecvenței crește de zece ori. Punctul de intersecție cu abscisa LACHH numit WSr frecvența de tăiere.
În construcția fazei logaritmice a frecvenței (LPC) unghiurilor caracteristice conta Y este axa verticală în scala normală în grade unghiulare. Pe abscisă este reprezentată grafic de-a lungul frecvenței W rămâne într-o scară logaritmică.
Este important să se țină cont de faptul că abscisa (L = 0) corespunde valorii k = 1. t. e. trecerea printr-un semnal de amplitudine legătură, fără a schimba amplitudinea. LACHH jumătate planul superior corespunde valorilor k> 1 (câștig amplitudine) și inferioară semiplanul - valorile A<1 (ослабление амплитуды).
2. Principalele tipuri de unități.
Tipuri de unități de comandă și reglare automată diferă în funcție de tipul de funcții de transfer (sau ecuații diferențiale), care determină proprietățile lor dinamice și caracteristici.
unități tipice sunt caracterizate prin ecuații diferențiale dinamice de ordinul nu mai mare de doi.
În funcție de tipul de ecuații diferențiale în teoria de control automat distinge între următoarele tipuri de bază de link-uri:
-inertialess (proporțională sau amplificând);
-inerțial ordinul întâi (sau aperiodice);
-inerția doilea ordin;
Principalele tipuri de link-uri sunt împărțite în trei grupe:
unități poziționale sunt acelea în care funcția de transfer
Polinoamele Bm (p) și An (p) sunt termeni constante egale cu 1, și anume, aceste legături sunt statice caracteristice Yust = k × Khust (la P = 0W (p) = k =), determină starea de echilibru - .. proprietăți pozițională .
În diferențierea elementului în expresia funcției de transfer nu este termenul constant al numărătorului, și anume o dată pentru elementul de diferențiere va B0 = 0 ..:
Acolo unde Bm-1 (p) este termenul constant egal cu 1, și K = - câștig.
Funcțiile de transfer ale componentei de integrare sunt, respectiv:
În cazul în care An-1 (p) are un termen liber egal cu 1.
Cunoașterea caracteristicilor tipice ale unităților necesare pentru sistemele de management de plată.
2.1. Ideal amplificând (inertialess) link-ul.
Ecuația și nivelul funcției de transfer:
Exemple sunt unitate portbusteni de viteze, un divizor de tensiune, senzorii de unghi, instantaneu et putere al. (Fig.9).
Fig. 9. Exemple de unități. Freewheeling
De fapt, nici o unitate freewheeling. De obicei, considerate ideale unități PAC inerție este mult mai mică decât inerția celorlalte verigi. Cele mai multe cazuri de diverși senzori și preamplificatoare. întârzierea inerțială a multor elemente de măsurare ale sistemelor automate (senzori de unghi nealiniere, senzori optici, senzori magneto) este mic, astfel încât acestea sunt considerate link-uri inertialess.
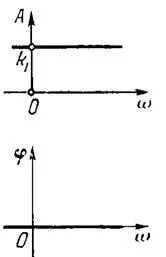
Figura 10. Caracteristicile de frecvență ale unității portbusteni
2.2. Inerțiale (aperiodic) link-ul.
Ecuația și nivelul funcției de transfer:
În cazul în care T - constantă de timp; K - rata de transmisie link-ul.
Exemple de inerție de unități (aperiodice) sunt motoare de curent continuu, când X (t) - tensiune de alimentare, și Y (t) - viteza unghiulară a arborelui W (t); motoare asincrone cu două faze; Amplificatori cu lag inerțial în considerare; corp masiv, dacă variabila de intrare pentru a contoriza numărul de căldură de intrare pe unitatea de timp și Q. ieșire - temperatura în orice punct din interiorul corpului, etc.). lanț L-R (Figura 11).
Figura 11. EXEMPLU link inerțial.
Figura 12. APFC elementul inerțial.
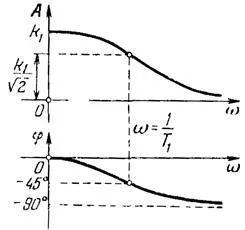
Figura 13. Răspunsul amplitudine-frecvență și fază a unității inerțial
Logaritmică caracteristică amplitudine-frecvență are forma:
Această caracteristică are asimptota:
Ultima asimptotă este înclinat linie dreaptă cu o pantă de -20 dB / decadă, iar primul - linia orizontală. Asymptotes se intersectează într-un punct Wc =. LACHH în sine aproape de aceste asimptote.
Pe o grilă logaritmică a frecvenței axa frecvenței colț Wc = (Fig.14). Pentru frecvențe mai mici decât montei, t. E. Când W<. можно пренебречь вторым слагаемым под корнем, тогда левее сопрягающей частоты можно заменить L(W) приближенным выражением
Această expresie corespunde liniei orizontale. Pentru frecvențe mai mari de împerechere W> în expresie pentru L (W) poate fi neglijată 1 sub rădăcină. Apoi, L (W) = 20lgk-20lg (WT). Al doilea termen este o linie dreaptă care se extinde oblic -20 dB / decadă. Linia frântă se numește LACHH asimptotic. Cea mai mare abatere de la LACHH exactă asimptotică aproximativ 3 dB la o frecvență de conjugare, adică..:
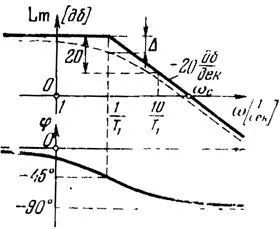
Figura 14. elementul inerțial LACHH.
Funcția de tranziție, conform ecuației unității de decizie pentru X (t) = 1 (t) și zero, condițiile inițiale este (Fig.15):
Figura 15. Funcția de tranziție a unității inerțial.
Constanta de timp determină panta T tangenta la începutul curbei (Figura 15). În consecință, valoarea T caracterizează nivelul persistență, adică. E. Durata tranzitorie. În teorie, acest proces de tranziție durează o perioadă nedeterminată. Practic, această legătură într-o tranzitorie timp să înțeleagă perioada de timp după care Ts inegalitatea:
Atunci când este aplicat link-ul semnalului de intrare X0 DC După tranzitorie coordonate Y (t) este conectat rigid la intrare:
2.3. O unitate oscilant.
Ecuația și nivelul funcției de transfer:
acceptat în general înregistrarea funcției de transfer a nivelului de vibrație sub formă de:
Amplitudine și de răspuns de frecvență de fază (Figura 16) link:
Figura 16. Caracteristicile de frecvență ale membrului oscilatorie.
Unitatea de răspuns de frecvență amplitudine logaritmică
La valori 0.5 Figura 17. Caracteristicile de frecvență logaritmică a membrului oscilatorie. În cazul în care X<0,5. то получается заметный максимум (рис.17). Максимум характеризуется превышением Hm Calculul simplificat pentru a găsi suficient de aproximare Hm (a se vedea figura 17) .: Funcția de tranziție a nivelului de vibrație este prezentată în figura 18. Figura 18. Funcția de tranziție a nivelului de vibrație. Atunci când X = 1, la un oscilații aperiodice proces degenerate. Când X = 0 oscilații sunt neamortizate (periodice), caz în care unitatea oscilatorie se numește management conservator. Exemple link-uri oscilatorii prezentate în fig.19. Figura 19. Exemple link-uri oscilatoriimateriale suplimentare