Studiul funcțiilor liniare

Browser-ul dvs. nu suporta iframe!

Funcția este unul dintre cele mai importante locuri din cursul algebra școlar, și are numeroase aplicații în alte științe. La începutul studiului, pentru a motiva, de a integra vă informa că nici un fenomen, nici un proces în natură nu poate fi studiată, nici o mașină poate fi proiectat și apoi să acționeze fără o descriere completă matematică. Un instrument pentru aceasta este o caracteristică. Studiul ei începe în clasa a 7-a, de regulă, copiii nu se îngropa în definiția. Mai ales concepte sunt dificil de acces, cum ar fi valorile de domeniu și gama. Folosind cunoscută relația dintre valorile în problemele mișcării, am schimba costul funcției lor în limba ținând legătura cu definiția sa. Astfel, conceptul elevilor unei funcții se formează la un nivel conștient. În aceeași etapă se realizează silitor pe concepte noi: domeniu, valori de domeniu, valoarea argumentul funcției. Utilizați formare în avans: introduce notația D (unde Y), E (y), se familiarizeze cu conceptul de funcție de zero (analitic și grafic), în rezolvarea exerciții cu porțiuni de semn constant. Cu cât mai devreme și mai mulți studenți întâlni cu concepte dificile, cu atât mai bine ei sunt conștienți în nivelul de memorie pe termen lung. În studiul funcției lineare, este recomandabil să se arate legătura cu soluția de ecuații și a sistemelor liniare, iar mai târziu cu soluția inegalităților liniare și sistemele lor. În timpul prelegerii, elevii primesc un bloc mare (modulul) de noi informații, astfel încât la sfârșitul materialului de curs este „presat“ și a pregătit un rezumat pe care elevii ar trebui să știe. abilități practice practicate în timpul exercițiilor folosind diferite metode, care se bazează munca individuală și independentă.

1. Unele informații cu privire la funcția liniară.

Funcția liniară este foarte frecventă în practică. Lungimea Rod este o funcție liniară a temperaturii. Lungimea șinelor, pod este, de asemenea, o funcție liniară a temperaturii. Distanța parcursă de pietoni, un tren, un vehicul cu motor, la o viteză constantă, - funcția liniară a timpului de călătorie.

Funcția liniară descrie o serie de legi fizice și dependențe. Luați în considerare unele dintre ele.

1) l = lo (1 + at) - dilatare liniară de solide.

2) v = Vo (1 + bt) - expansiunea volumetrică a solidelor.

3) p = Po (1 + at) - dependența rezistivității pe fire solide de temperatură.

4) v = Vo + la - viteză accelerată uniform mișcare.

5) x = Ho + vt - coordonata mișcare uniformă.

Problema 1. Se determină o funcție liniară de date tabelare:

Constructing pereche obținută (x, y) în planul de coordonate și conectarea acestora la fiecare funcție în parte (am luat valoarea lui x în 1, dacă reducerea pas, punctele sunt aliniate în mod frecvent, iar dacă pasul este aproape de zero, atunci punctele vor fuziona într-o linie continuă ), observăm că punctele de linia de sus în linie dreaptă, în cazul 1) și cazul 2). Datorită faptului că funcțiile sunt selectate în mod arbitrar (construcția grafică singur y = 0,5x - 4, y = x + 5), putem concluziona că graficul este o funcție liniară dreaptă. Folosind proprietatea directă care trece prin două puncte doar o singură linie dreaptă este suficientă pentru construirea unei directe să ia două puncte.

6.Iz geometrie este cunoscut faptul că liniile pot fie suprapunere sau să fie paralele. Noi examinăm poziția relativă a graficelor de mai multe funcții.

1) y = -x + 5, y = -x + 3, y = -x - 4; 2) y = 2x + 2, y = x + 2, y = -0,5x + 2.

Am construi un grup de grafice 1) și 2) și pentru a trage concluzii.

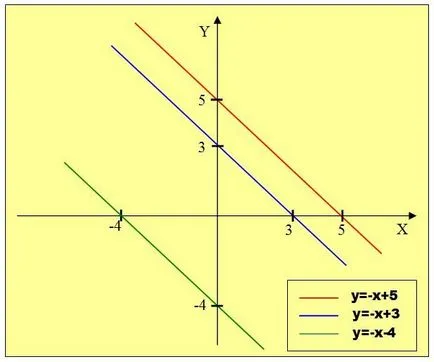
Graficele funcții 1) dispuse în paralel, examinarea formulei, observăm că toate funcțiile au aceiași coeficienți de x.

Funcții Diagramele 2) se intersectează într-un punct (0, 2). Investigând formula, observăm că diferite raporturi, iar numărul b = 2.

Mai mult, nu este dificil de a vedea că liniile definite de funcții liniare cu k> 0 formează cu direcția pozitivă Ox - unghi ascuțit cu k <0 unghi obtuz. Prin urmare, coeficientul k se numește panta.

7. Luați în considerare cazurile particulare de funcții liniare, în funcție de coeficienții.

1) În cazul în care b = 0, atunci funcția ia forma y = kx, atunci k = y / x (raportul arată cât de mult timp diferit sau ce parte a lui y pe x).

Funcția de forma Y = kx, numit direct proporțional. Această funcție are toate proprietățile unei funcții liniare, caracteristica sa este. că, atunci când x = 0, y = 0. Graficul de proporționalitate directă trece prin punctul de origine (0, 0).

2) Dacă k = 0, atunci funcția ia forma y = b, care este, pentru orice valoare a lui x, funcția are aceeași valoare.

Funcția de forma y = b, numită constantă. Graficul funcției este o linie dreaptă care trece prin punctul (0; b) paralelă cu axa Ox, graficul b = 0 o funcție constantă coincide cu axa x.

1. Definirea funcțiilor formei Y = kx + b, unde k, b - unele numere x -argument, valoarea Y- a funcției se numește o funcție liniară.

Graficul unei funcții liniare este o linie dreaptă care trece prin punctul (0; b).

2. În cazul în care b = 0, atunci funcția ia forma y = kx, numită proporționalitate directă. Graficul de proporționalitate directă trece prin origine.

3. Dacă k = 0, funcția ia forma y = b, se numește constantă. Funcția Schedule Timpul trece prin punctul (0; b), paralel cu axa abscisă.

4. Pozițiile relative ale graficelor de funcții liniare.

Dacă k1 = k2. grafica sunt paralele;

Dacă și k2 nu k1 sunt egale, graficele se intersectează.

5. Exemple de funcții liniare grafurilor cm. Deasupra.