Stabilirea unui elipsoid de revoluție

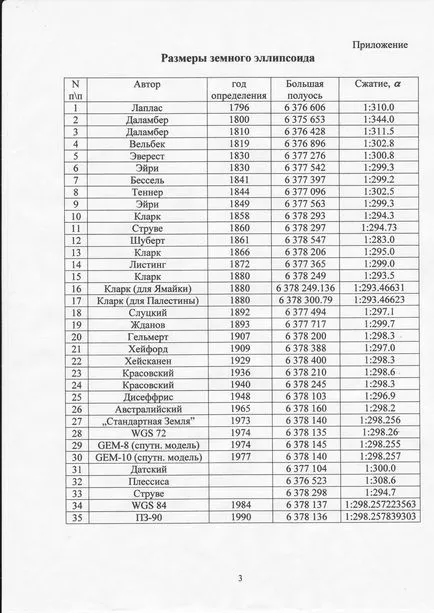
Sarcină. Elipsoide pentru doi parametri indicați în anexă pentru a calcula restul principalilor parametri și să le compare cu parametrii elipsoidului WGS 84. prezintă schematic elementele individuale din desen.

Elipsoid de rotație, elemente și relațiile dintre ele sale.

Elipsoid de rotație se numește corpul geometric format prin rotirea unei elipse în jurul axei sale minore. Ecuația suprafeței în formă canonică de rotație este dată de:

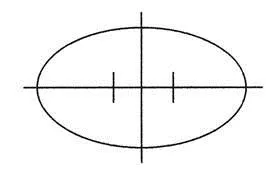
În cazul în care - axa mare sau ecuatorială elipsoidului, - semiaxa mică sau polar (Figura 1).

Secțiunile de suprafața unui avioane elipsoidale perpendicular pe axa de rotație, reprezintă un cerc numit paralele. Cele mai multe plane paralele care trece prin elipsoid despre centru, numit ecuatorului. Ecuatorul împarte elipsoid în două jumătăți egale: la nord și sud.

Un plan care trece prin axa secundară a elipsoidului, numit planul meridian, iar suprafața lor secțiune transversală a elipsoid - meridianele.

sectiunea Meridian sunt elipse. distanta de la

centrul elipsei fiecărei focare, egal, numit excentricitatea liniară, și raportul excentricitate liniar pe o axă mare sau mică - excentricitatea elipsei. distinge în consecință, primul și al doilea meridian elipsa excentricitatea:

Primul excentricitatea - (2)

A doua Excentricitatea - (3)

Elemente liniare - semi-axa majoră și minoră - elipsoidului definesc dimensiunile și excentricitatea - forma, cu alte cuvinte, mai mult sau mai puțin aplatizat la poli. Cu cât mai mare diferența dintre majore și minore semi-axe, cu atât mai mare excentricitate, și invers. În sfera este zero.

Forma elipsă determină, de asemenea, dimensiunea relativă a celuilalt așa-numita aplatizare, polar, sau pur și simplu comprima elipsoid, calculat conform formulei: (4)

După cum rezultă din formula (1), un elipsoid de revoluție este complet determinată de două elemente - majore și minore semi-axe. În schimb axa minoră este adesea folosit de compresie sau de excentricitate. Unul dintre cele două elemente specificate trebuie să bată linia.

Împreună cu (2) - (4), există următoarele relații între elementele unui elipsoid:

Ele rezultă direct din formulele (2) și (3). Dacă pui:

Prin transformări simple, putem obține:

Raza de curbură polară (uneori numită principal) este egal cu:

. Razele de curbură principale la un moment dat, sunt:

M - într-un plan meridian,

N - în primul plan vertical (primul vertical - planul care trece prin normala la ortogonale elipsoid cu planul meridian),

- raza medie de curbură. La ecuator, raza de curbură meridianul (M) este minimă, ecuatorului (N) și raza medie de curbură (R), determinat prin expresiile:

Din formulele (4) și (7), care provin din.

Pentru elipsoid terestru, cu calcule de viza inapoi, pot fi luate :.

Valori sferice Geodezie si prima ordine, și - a doua ordine, și așa mai departe.

Vizați elipsoid de rotație - 4.5 din 5 bazat pe 2 voturi