Solutia problemelor pe ecuații diferențiale și serii, pagina 3

O serie alternativ este, prin urmare, prin caracteristica corolar Leibniz. Evident, al treilea termen al seriei, astfel încât n = 2 și până la 0,001:

.

Pentru a calcula, de exemplu, trebuie să fie setat la radiani.

b) Pentru a calcula prima prezent, astfel încât să putem scrie:

.

În continuare, aplicăm seria binomială, în care cred. În cazul nostru :.

Am pus într-un număr, atunci

,

.

Din moment ce al treilea membru, prin urmare, și cu o precizie de 0,001 :.

4.11. Calculul integralelor folosind serii

Deoarece termenul serie de putere de termen poate fi integrat pe orice segment situată în intervalul de convergență, apoi prin extinderea integrandul în seria de putere este posibil să se găsească o valoare aproximativă a definit integral.

Exemplul 1. Se calculează aproximat cu o precizie de 0,001 :. integral definit

Decizie. Integrandul este de așa natură încât primitivă sa nu poate fi exprimată în termeni de funcții elementare. Se aplică la un număr, obținem:

,

,

din moment ce al treilea membru obținut serie alternativ este mai mic de 0,001.

Exemplul 2. Se calculează aproximativ până la 0,01 integral:

.

Decizie. Funcția Antiderivative, de asemenea, nu poate fi exprimat în termeni de funcții elementare:

,

pentru orice x (aici am folosit o serie Maclaurin pentru funcția)

Pentru a evalua utilizarea restului rezultatului caracteristicii Leibniz eșuează, deoarece o serie alternantă nu se obține. Procedați după cum urmează:

.

Consolele au primit suma de progresie geometrică infinit, care este de 1 :. Prin urmare.

Calculând dreptul acestei inegalități pentru diferite n (n = 1, 2, 3, 4), observăm că pentru n = 4 :. Prin urmare, pentru a calcula integrala pana la 0.01 este suficient pentru a lua S4. și anume

.

4.12. Soluție aproximativă de ecuații diferențiale

Uneori integra precis ecuația diferențială nu reușește. În acest caz, este convenabil să caute o soluție sub forma unei serii de puteri.

Exemplul 1 este dat ecuație diferențială. Găsiți o anumită soluție ce satisface condiția inițială y (1) = 1, sub forma unei serii Taylor (luând primii 5 membri).

Decizie. Lăsați soluția este

Condiția inițială y (1) = 1, primul termen al acestei serii. Substituind x = 1 și y = 1 în ecuație, obținem :.

Ne diferentiem ecuația originală:

, , ,

, ,

etc. Înlocuim valorile găsite din serie, obținem:

Exemplul 6 2. Găsiți primii termeni în soluțiile de expansiune seria de putere ale ecuației diferențiale care satisface condițiile inițiale y (0) = -2.

Decizie. Deoarece x0 = 0, atunci soluția este solicitată sub forma unei serii Maclaurin

.

Având în vedere că y (0) = -2. Substituind în această ecuație condițiile inițiale, obținem: Prin diferențierea ecuația originală, vom găsi succesiv:

, , ,

, , .

Substituind valorile găsite în serie, obținem:

.

4.13. seria Fourier

Exemplul 1 extins într-o funcție Fourier f (x), având o perioadă predeterminată și 2p în intervalul (-p p] după cum urmează .:

Decizie. f funcție (x) are un punct de discontinuitate (fig. 4.2).

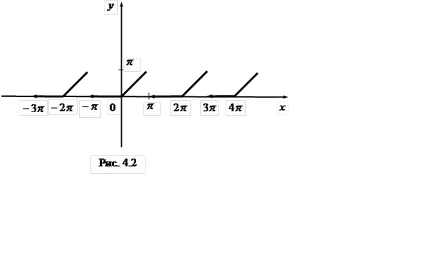
Deoarece f (x) monotonă și are porțiuni pe intervalul [-p. p] este doar un punct de discontinuitate de primul tip (), apoi toate punctele x de continuitate a lui f (x) poate fi extinsă într-o serie Fourier. Vom găsi o serie de factori:

.

,

n i N. Substituind acești coeficienți într-un rând, obținem:

pentru toți, Kj Z. Numărul de puncte suma găsite:

.

Exemplul 2 extins în serie Fourier funcție periodică f (x), cu perioada
2l = 4, definită pe intervalul (-2, 2] de ecuația: f (x) =.

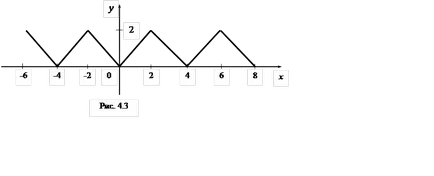
Decizie. Funcția f (x) este definit și continuă pe axa reală întreg și pe segmentul monotonă pe porțiuni [-2, 2] (fig. 4.3).

Se calculează coeficienții unei serii Fourier:

,

.

La calcularea proprietate utilizarea bn a unei funcții de ciudat:

,

deoarece integrandul este ciudat. Seria Fourier pentru funcția converge la această funcție pentru toate x. deoarece f (x) este continuă pentru toate x. Astfel,

.

1. Ecuatii diferentiale ordinare. 4

1.1. Probleme care conduc la ecuații diferențiale ordinare. 4

1.1.1. Problema căderii libere a corpului. 4

1.1.2. Problema tranzitorii în circuitul electric. 5

1.1.3. Problema dezintegrarii radioactive. 6

1.2. definiții și concepte de bază. 6

1.3. Sensul geometric al ecuației. 9

1.4. Clasele principale ale primelor ecuații diferențiale de ordinul. 10

1.4.1. ecuații diferențiale cu variabile separabile. 10

1.4.2. ecuații diferențiale. omogeni 11

1.4.3. Ecuatii diferentiale liniare. ecuația Bernoulli. 12

1.4.4. ecuație diferențială ordinară. 14

1.5. Ecuații diferențiale de ordin superior. 17

1.5.1. Ecuațiile care permit reducerea ordinului. 17

1.5.2. ecuatii diferentiale liniare de ordinul n. 21

1.5.3. Liniare omogene ecuații diferențiale a doua ordine cu coeficienți constanți. 24

1.5.4. Linear ecuație diferențială neomogenă de ordinul n-lea. 28

1.6. Un sistem de ecuații diferențiale ordinare. 33

1.6.1. Metoda de eliminare a necunoscutelor. 34

1.6.2. Sisteme de ecuații diferențiale liniare cu coeficienți constanți. 36

2. seria numerică. 39

2.1. Conceptul unei serii numerice. 39

2.2. Suficientă pentru convergența serie cu termeni pozitivi. 42

2.3. Alternarea rânduri. O serie de alternativ. 48

3. Seria funcțională. 52

3.1. Conceptul de serii funcționale. 52

3.2. Seria de putere. 54

3.3. Din seria de putere. 58

3.4. seria Taylor și Maclaurin. 59

3.5. Utilizarea serie de puteri. 64

3.6. serii Fourier. 67

4. Soluția problemei. 74

4.1. Ecuațiile diferențiale ale primului ordin cu variabile separabile. 74

4.2. ecuație diferențială Omogen. 74

4.3. ecuație diferențială liniară a primului ordin. 75

4.4. Ecuații diferențiale de ordin superior, care permit reducerea ordinului. 77

4.5. a doua ecuații liniare diferențiale de ordinul cu coeficienți constanți. 78

4.6. Sisteme de ecuații diferențiale liniare cu coeficienți constanți. 78

4.7. Semne de convergenta seriilor cu termeni pozitivi. 78

4.8. Alternarea rânduri. tag-ul Leibniz. 78

4.9. Seria de putere. seria Taylor și Maclaurin. 78

4.10. Calcularea valorii aproximativă a funcției. 78

4.11. Calculul integralelor folosind serii. 78

4.12. Soluție aproximativă de ecuații diferențiale. 78

4.13. serii Fourier. 78

Testul. 91

Reguli de execuție și de încercare de înregistrare. 91

PROBLEME PENTRU testare. 92

întrebări examen. 96