Seturi de echivalență - studopediya

Definiția 1.2. În cazul în care fiecare element al A este mapat la un element unic de B și, în același timp, fiecare element al lui B este mapat la unul și numai un element al lui A. este declarat a fi între seturile A și B există un unu la unu corespondență. Seturile de A și B, în acest caz, se spune că este echivalent sau equicardinal.

Seturile de echivalenŃă sunt desemnate după cum urmează: A

Setul de echivalență are proprietatea tranzitivității.

Să ne dovedesc această proprietate. Din moment ce un

B. atunci pentru orice element de Î Și există un element unic b Î B. Dar, din moment ce B

C. atunci pentru fiecare element b Î B există un element unic c Î C. asociat cu acel element de membru Î A. Acest lucru înseamnă că, pentru fiecare element de Î Și există un element unic c Î C, și pentru fiecare element c Î C, există doar un singur element al Î A. Prin urmare, A

Este evident că două seturi finite sunt echivalente dacă și numai în cazul în care numărul de elemente din ele în mod egal. De exemplu, mulțimea A = și B = x. y. z> echivalent, A

B. A-la-unu corespondență poate fi stabilită între elementele 4 și x. 5 și y. 6 și z.

O pluralitate de putere finită (notate çA ç) Este numărul de elemente din acest set. De exemplu, puterea este setată A = çA ç= 2.

Anterior (Sec. 1.1), am examinat multimea toate subgrupurile multimea A este denumit set de grade și este desemnat P (A). O pluralitate de P (A) este format din 2 n elemente. Astfel, çP (A) ç = 2 n.

Luați în considerare problema de determinare a puterii de a combina seturi de n finite.

Fie n = 2 și A și B - două seturi intersectate. Dovedim folosind diagrama Euler - Venn următoarea relație:

çA ÈB ç= çA ç+ çB ç- çA ÇB ç. (1.1)

Fig. 1.3 vedem că

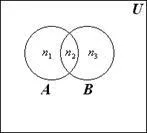
Formula (1.1) este valabil și pentru cazul în care o pluralitate de A și B nu se intersectează. În acest caz,

çA ÈB ç= çA ç+ çB ç.

Să presupunem că n = 3 și A. B și C - cele trei seturi se intersectează. În acest caz, următoarea relație deține:

çA ÈB È C ç= çA ç+ çB ç+ çC ç- çA ÇB ç- çA ÇC ç- çB ÇC ç+ çA ÇB ÇC ç. (1.2)

Fig. 1.4 vedem că

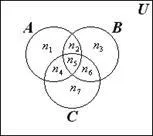
Aceasta dovedește formula (1.2).

Formula (1.2), este valabil și pentru cazul în care o pluralitate de A. B și C sunt disjuncte. În acest caz,

çA ÈB È C ç= çA ç+ çB ç+ çC ç.

În general, capacitatea de asociere a seturilor de n se determină prin formula:

Această formulă este derivat prin inductie. [3].

În cazul în care seturile Ai sunt disjuncte, adică, Ai Çaj = Æ, I ¹ j, obținem un caz special cu formula (1.3):

În general, inegalitatea

Noțiunea de echivalență este de asemenea potrivit pentru seturi infinite. Să presupunem, de exemplu, A = n, ...>, B = n. ...>. apoi, A

B. A-unu la unu corespondență este stabilită prin elementul regula n Î A corespunde cu un element - n Î B. și anume n «- n.

B. A-unu la unu corespondență se stabilește conform regulii: n «2 n.

A = n, ...> - mulțimea numerelor naturale, B = n. ... - 2, -1, 0, 1, 2, ..., n. ...> - mulțimea tuturor numerelor întregi.

Rescriem mulțimea B, după cum urmează:

B = n. n. ...>, astfel încât 0 este la prima locație, a doua -1, 1 pe al treilea, al patrulea și -2 etc. Este ușor de observat că numerele negative vor sta pe teren cu numere chiar și 0 și numere pozitive - în câmpul cu număr impar. Prin urmare, unu-la-o corespondență între seturile A și B este setat conform regulii: pentru fiecare n ³ 0 element a = 2n +1 pluralității A (adică un element ciudat) corespunde elementului b = n pluralității B; a = elementul 2n al pluralității A (adică elementul chiar) corespunde elementului b = -na pluralitatea B. Astfel, realizată de o corespondență între seturile A și B. 1 „0, 2“ 1, 3 „1 , 4 „-2, etc.

Exemplele 1.18 și 1.19 indică faptul că setul poate fi echivalent cu subsetului. Astfel, în exemplul 1.18 B Ì A. și Exemplul 1.19 A Ì B. Și, de fapt, în ambele cazuri A

Stabilirea echivalenței de seturi, și anume, să stabilească o corespondență unu-la-unu între elementele lor pot fi moduri diferite. Fig. 1-5 arată că setul de puncte din două segmente [a. b] și [c. d] echivalent.

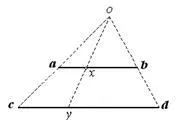
În același set modul poate fi setat puncte de echivalență a două sloturi. In figura 1.6 se arată că orice set de puncte ale intervalului (a. B) este echivalentă cu o multitudine de puncte peste linia.

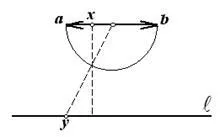
Pentru a stabili echivalența dintre cele două seturi pot fi folosite următoarea teoremă.

Bernstein teorema. Dacă o pluralitate de A este echivalentă cu o parte a setului B. set B este echivalent cu porțiunea din multitudinea de set A. A și B sunt echivalente.

Bernstein aplică teorema pentru a dovedi că punctul de setare al oricărui segment este echivalent cu o multitudine de puncte de orice interval.

Fie A = [a. b] - interval arbitrar, și B = (c d.) - un interval arbitrar.

Astfel, condițiile de teorema lui Bernstein. Prin urmare, A

Deci, toate intervalele, segmentele, și linia întreg echivalent.