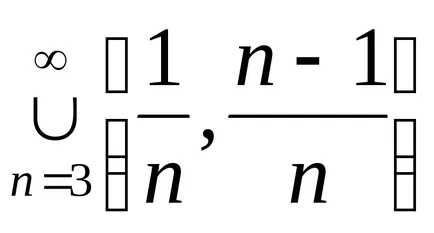seturi de circuite

Definiția 3. Fie X - spațiu metric, M  X și H. Punctul A se numește tochkoyM limită. în cazul în care în orice moment există o vecinătate a M \ a>. Acest lucru înseamnă că, în orice vecinătate și există puncte de M diferite de la o.

Note. 1. Punctul limită este cum să aparțină și nu aparțin setului. De exemplu, 0 și 1 sunt o multitudine de puncte limită (0,2), dar nu este primul membru și al doilea element.

Set punctul M nu poate fi și punctul limită. In acest caz, se numește punct izolat M. De exemplu, 1  punct izolat (1,0) .

Dacă punctul limită și nu face parte din setul M există o secvență de puncte xn M. convergente către și în acest spațiu metric. Este suficient pentru a lua bilele deschise la punctul de raza 1 / n și alege de la fiecare punct aparținând M. mingii În schimb, în ​​cazul în care există o astfel de secvență, punctul este limita.

DEFINIȚIE 4. Închiderea stabilită M este unirea M cu punctele sale limită stabilită. denumire

.

Rețineți că de închidere cu bilă nu coincide neapărat cu mingea închisă aceeași rază. De exemplu, într-un spațiu discret al circuitului bilă B (a, 1) este egal cu mingea (format dintr-un punct a) in timp ce mingea închisă

(A, 1) este întreg spațiul.

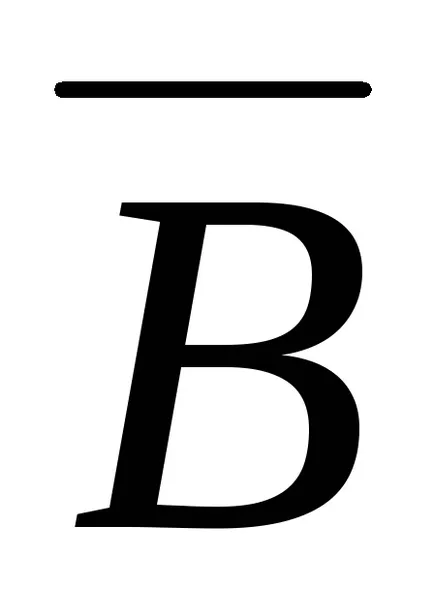
Vom descrie unele proprietăți ale seturilor de circuit.

M 

. Acest lucru rezultă în mod direct din definiția închiderii.

Dacă M este  N.

. Într-adevăr, eslia ,un M. apoi, în fiecare cartier există un punct de M. Acestea sunt punctele de N. Prin urmare, un . Pentru punctele Chg este clar din definiția.

.

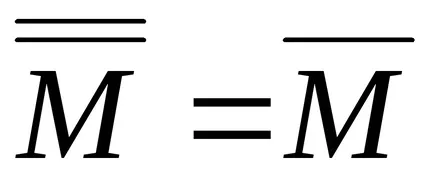
Închiderea setului gol este gol. Acest acord nu rezultă din definiția generală, dar este firesc.

DEFINIȚIE 5. Setul M  X se numește închisă. dacă

= M.

O MX pluralitate numită densă în X, dacă

= X.

DEFINIȚIE 6. Punctul A este punctul intern al setului M, în cazul în care B (a, r) ​​M pentru unele r pozitiv, t. Punct E. intern inclus în setul cu un anumit cartier. Punctul a este punctul exterior al setului M. Dacă bila B (a, r) ​​H / M pentru unele r pozitiv. t. e. Punct intern nu este inclusă în setul cu un anumit cartier. Punctele care nu sunt nici puncte, internă sau externă ale M. numite limite.

Astfel, punctele de frontieră sunt caracterizate prin aceea că, în fiecare punct din vecinătatea lor este atât în ​​interiorul cât și în afara M.

Propoziția 4. Pentru a seta este deschisă dacă și numai dacă toate punctele sale erau interne.

Exemplele închise seturi sunt într-o linie dreaptă [a, b], [a, ). Deschideți - (a, b), (a, ). Setul [a, b) nu sunt deschise și nu închise (conține nici un punct limită b. Un set complementar conține nici un punct limită a). Toate spațiu metric X și vidă  5 din acord sunt ambele deschise și închise. Spatiul metric discret este un subset de ambele deschise și închise.

Proprietatea 3 circuite care urmează combinarea a două (și, prin urmare, orice familie finită) seturi închise închise. În același timp, unirea unei familii infinit de seturi închise nu pot fi închise, de exemplu,

= (0, 1).