sens geometrica si mecanica a derivatului

Cu calcularea derivatului întâlnim ori de câte ori este necesar pentru a determina rata de schimbare a unei funcții de cantitate - în funcție de modificările în celelalte valori - variabila independentă.

funcțiile centrale ale unei rate de schimbare în tranziția de la valorile variabilei independente la valoarea funcției raportul increment este chemat la incrementa variabila independentă, adică

Rata Adevărat sau instantanee de schimbare a funcției la o anumită valoare a variabilei independente este limita la care tinde rata medie de schimbare a funcției tinde la zero creștere a argumentului:

Sensul mecanic al derivatului

(Sens mecanic al derivatului)

Având în vedere o cale de mișcare a unui punct. Viteza punctului materialului în timp este derivata modului în timp:

Sarcină. Corpul se mișcă într-o linie dreaptă, în conformitate cu (m). Se determină viteza la momentul respectiv cu.

Decizie. Viteza dorită - este un derivat al modului, adică,

La un anumit moment în timp

Mai multe exemple de derivați de luare a deciziilor online

semnificația geometrică a derivatului

Funcția derivat, calculată la o valoare dată, egală cu tangenta unghiului format de direcția pozitivă și direcția pozitivă a unei tangente la graficul functiei la punctul cu abscisa:

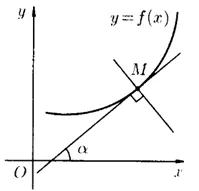
derivat Geometric este panta tangentei la graficul funcției în punctul.

Sarcină. Figura prezintă un grafic al №1 și tangenta la acesta la punctul cu abscisa. Găsiți valoarea.

Decizie. Semnificația geometrică a derivatului obținem că

Am găsit unghiul. Luați în considerare un triunghi - un dreptunghiular, isoscel. Apoi, așa

Și rezultă că

Mai multe exemple de derivați de luare a deciziilor online