Reguli pentru compilarea sknf
Tabelul conține trei rânduri cu valori zero ale funcției. Aceste linii 2, 4 și 6.
Facem o preformă cu formula - în partea dreaptă a trei disjuncția de scriere (fiecare în paranteze)
.
Acum negație aplicată asupra variabilelor având o valoare de 1 în seturile respective,
.
B) forme normale disjuncte și conjunctive
După cum se poate observa, o funcție logică poate fi reprezentat de cel puțin două formule - PDNF și SKNF. Din aceste formule, prin transformare (de exemplu, minimizarea) poate fi preparat un număr de formule în formă normală disjunctivă (DNF) sau în formă normală conjunctivă (CNF).
formă normală disjunctivă a funcției de logică se numește disjungerea orice număr de conjuncțiilor elementare.
forma normala conjunctiva a unei funcții logice este numită o conjuncție cu orice număr de disjunctii elementare.
Ca un exemplu al extragerii funcției de conversie
Astfel, o funcție logică poate avea mai multe formule, dar întotdeauna formula descrie o funcție logică. Această diferență între conceptele de funcții logice și formule, reprezintă.
D) Mintermy, makstermy și proprietățile lor
o expresie formată din variabile, constante, simboluri, operații și, posibil paranteze se numește un termen.
Mintermom numit elementară maximă conjuncție rangar = n. că este, o conjuncție, care include o dată toate variabilele, cu sau fără negarea negației. Pentru N variabile pot genera 2 n mintermov. Pentru N = 1, va exista două: o și

1. Suma (disjuncție) toate variabilele mintermov n este 1.
când n = 3 ... (dovedesc tine).
De aceea, mintermy denumite și constituenții (componentele) ale unității.
2. Produsul (conjuncția) dintre cele două variabile mintermov n este 0.
Într-adevăr, dacă mintermy nu identice, atunci cel puțin o variabilă într-o singură parte, fără negare, iar în celălalt cu negație, deci în produs, o pereche de forma
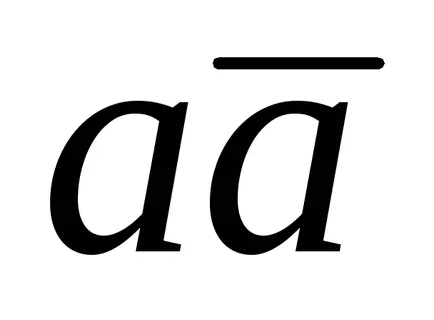
Makstermom numit elementar maxim disjuncție rangar = n. că este, disjuncției, care include o dată toate variabilele, cu sau fără negarea negației. Pentru N variabile pot genera 2 n makstermov. Pentru N = 1, va exista două: o și

1. Produsul (conjuncția) tuturor variabilelor makstermov n este 0.
când n = 3 ... (dovedesc tine).
De aceea, makstermy denumite și constituenții (componentele) de la zero.
2. Suma (disjuncției) a două variabile diferite makstermov n este 1.
Într-adevăr, dacă makstermy nu identice, atunci cel puțin o variabilă într-o singură parte, fără negare, iar în cealaltă cu o negare, deci suma lor, o pereche de forma
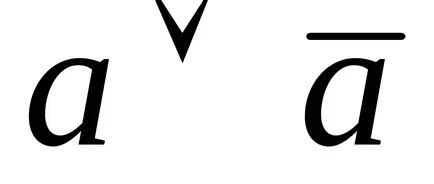
minterm și maksterm termeni sunt explicate după cum urmează.
Minterm ia valoarea 1 numai pe un singur set de variabile (în alte seturi și lor 2 n - 1, este 0), iar acesta are un element - .. O suprafață minimă pe Carnot (vezi Tabelul 12.4 harta și unde elementul 1 umplut cu vopsea gri, o hartă Karnaugh, a se vedea. numărul de curs 13).