Recalcularea mol fracție în masă

Conform datelor pe care le construi graficul izobară de cristalizare temperatura de pornire a sistemului compoziției în coordonate T - NA (Fig.1).

fracții molare retratarea în masă

fracțiunea de masă a substanței într-un sistem cu două componente este raportul dintre masa substanței la greutatea totală a sistemului.

Împărțind această ecuație în greutate component A, obținem

Reprezentarea componentei greutate ca produs al greutății moleculare componente de numărul de moli obțină

Masa molară a componentei în sistem cu două componente este raportul dintre numărul de moli de component la numărul total de moli ai sistemului.

Prin urmare, raportul dintre fracția molară a componentelor este egal cu raportul dintre numărul de moli ai componentelor respective.

Substituind ecuația (2.5) până la (2.3), obținem formula pentru conversia fracția molară a unei componente într-o masă:

Rezultatele de conversie sunt prezentate în tabelul. 2.1.

Datele obținute construi diagrama izobară în coordonate T - A (Figura 2).

Prin cristalizare diagramă construirea curbelor de răcire (Figura 3) variantă a sistemului la punctele aparținând curbelor de date descrise de regula fază Gibbs.

Dacă o presiune heterogen sistem și temperaturii în toate fazele aceleași, iar numărul de moli tuturor componentelor din fiecare fază este constantă, atunci aceasta se numește starea fazei de echilibru. starea de echilibru de fază este potențial chimic egal al componentei în fază la valoarea sa în orice altă fază.

Pentru a descrie starea sistemului eterogen, este necesar să se cunoască temperatura, presiunea și concentrația componentelor din fiecare fază. Dar dacă sistemul stabilit de echilibru de fază, singura parte a acestor variabile sunt independente, deoarece concentrațiile componentelor în fazele individuale sunt conectate prin ecuația (4.1). Numărul de variabile independente necesare pentru a descrie starea de echilibru a unui sistem eterogen, numit varianța, sau numărul de grade de libertate termodinamice a sistemului. Variabilitatea sistemului (# 969;) definește de asemenea un număr de variabile independente, care pot fi în mod arbitrar (în anumite limite) pentru a schimba, fără a perturba starea sistemului, adică, fără a schimba numărul și tipul de faze în ea. Variația sistemului depinde de numărul de componente și este determinată de regula fază Gibbs

# 969; = K - F 2 - R - L. (4.2)

unde K este - numărul de componente;

R - numărul reacțiilor chimice în sistem;

L - numărul de ecuații suplimentare de cuplare între concentrațiile componentelor.

În această lucrare, considerăm un sistem care nu are reacții chimice și fără ecuații suplimentare de constrângere, care este, de asemenea investigate, la o presiune constantă. Prin urmare, ecuația Gibbs va fi:

Folosind această ecuație, vom calcula variația curbelor de răcire (Figura 3) și diagrama fuzibilitate (Fig.1). Calculul este dat in continuare (figura 3)

Concluzia regula pârghiei.

Masa cristalelor precipitate din topitură în timpul răcirii, poate fi determinată folosind regula pârghiei. Concluzia acestei reguli este dată pentru punctul O. Pentru această formă ecuația echilibrului material al componentei B la o temperatură constantă.

m # 966; B (O) = mrastvora # 966; B (L) + mkristallov # 966; B (K) (5.1)

Substituind ecuația (5.2) până la (5.1), obținem

(+ Mrastvora mkristallov) # 966; B (O) = mrastvora # 966; B (L) + mkristallov # 966; B (K) (5.3)

Rezolvarea ultima ecuație pentru masa de cristale:

mrastvora # 966; B (O) + mkristallov # 966; B (O) = mrastvora # 966; B (L) + mkristallov # 966; B (K)

Din ecuația rezultată este o rată de:

$Recalcularea mol fracție în masă$

;

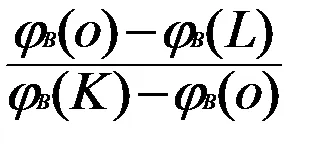
CO = 20, OL = 45 = 2-mrastvora MKR

Să considerăm sistemul de echilibru constând în două faze - lichid și solid. Lăsați fiecare fază este adevărata soluție. Când echilibrul fazei

Potențialul chimic al unei componente în fiecare fază depinde de temperatura, presiunea și activitatea componentelor

În cazul în care μk 0, x (T, p) și μk 0 TV (T, p) - potențial chimic al lichidului component pur și în stare solidă, la o anumită temperatură și presiune;

ak si ak x tv - componentă activă în fazele de echilibru.

Luând în considerare (6.1) și (6.2), (4.1) poate fi transformată

La temperatură și presiune constantă

Din (6.4) rezultă că raportul componentului activ în fazele la echilibru la temperatură și presiune constantă, - legea echilibrului fazei.

Dacă la o anumită temperatură și presiune adăugat la una dintre fazele unui număr de k componente, aceasta va cauza redistribuire între faze, astfel încât raportul componentului activ în echilibrul constant din nou rămân neschimbate. Când temperatura sau presiunea modificări, sistemul va merge la o altă stare de echilibru, în care raportul de schimbare a componentului activ în fazele la echilibru și se va deplasa echilibrul.

Să considerăm, ca o modificare a temperaturii la presiune constantă o modificare afectează compoziția fazelor de echilibru. Pentru a exprima acest lucru în ecuația (6.3) prin fracțiile molare ale activității

Ecuația rezultată pentru temperatură diferențiată

Conform ecuației Gibbs-Helmholtz

în care - schimbarea potențialului chimic al componentei pure atunci când se trece de la solid la lichid;

- căldura molară a componentei de topire.

Folosind ecuația (6.7), obținem

Ultima ecuație în formă diferențială descrie efectul temperaturii asupra compoziției de echilibru sub defazaj izobară de echilibru, în timpul tranziției de la starea de echilibru la o singură temperatură în stare de echilibru la o temperatură diferită.

Componente solide soluții similare în formă proprietăți fizice și chimice și au același tip de cristal cu zăbrele. În cazul în care componentele în fază solidă sunt insolubile unul în celălalt, apoi soluția lichidă a evidențiat cristale ale substanței pure. În acest caz, există un echilibru: soluție lichidă cu două componente și cristale de un component (Nk tv = 1, # 947; k tv = 1), iar ecuația devine

Integrarea acestei ecuații, presupunând că aceasta nu depinde de temperatura

Aici și - temperatura de cristalizare a soluției component pur și temperatura de cristalizare a substanței pure. Ecuația (6.10) în formă integrală descrie efectul temperaturii asupra echilibrului „soluție lichidă - component cristale“. În cazul în care faza lichidă aproape de proprietățile ideale ale unei soluții de (# 947; k x = 1), atunci ecuația (6.10) este scrisă sub forma

Ultima ecuație se numește ecuația Schröder, în care - fracția molară a componentei în soluția lichidă este situată în ecuația cu cristalele, adică concentrația unui component într-o soluție saturată sau solubilitatea unei componente la k

Din ecuația Schroeder, care, în cazul soluțiilor ideale solubilității componentelor crește odată cu creșterea temperaturii.

ecuația lui Schroeder pot fi folosite pentru diferite sarcini:

1. Atunci când cunoscută temperatură de cristalizare a componentului pur și compoziția specificată de temperatura de topire de cristalizare, atunci ecuația (6.11) se poate calcula căldura de topire a componentelor k molare:

și pot fi identificate prin diagrama sistemului.

2. Dacă căldura molară a componentei de fuziune este cunoscută, ecuația (6.11) poate fi rezolvată pentru temperatura la care topitura cristalelor devin proeminente component k:

3. Calcularea scăderea temperaturii de cristalizare a componentelor se topește de compoziție diferită -:

Ecuația (6.11) pentru componenta A:

Din ecuația (6.14)

Pentru soluții diluate (Nk tv → 1, # 947; k TV → 1)

În soluții diluate. astfel încât ultima ecuație poate fi scrisă cu ajutorul d-scara

Cantitatea în ecuațiile (6.15) și (6.16) la valori care exprimă compoziția soluției. Chemat constantă cryoscopic care depinde numai de proprietățile componentei A.

1. Kiseleva EV Karetnikau GS Kudryashov IV Colectarea de exemple și probleme în chimie fizică. Proc. Reduceri pentru procesul Chem-primar. vuzov.- ed 5-a. Revizuit. și ext. - M. Executiv. săpt. 456 p 1983.-.

2. Prelegeri de Chimie Fizică (profesor asociat Uritskaya AA).

Equilibrium „Chitul (topi) - cristale“ într-un sistem cu două componente a

Profesor: Uritskaya AA

1. Sarcina de proiect de curs

1.1. problemă condiție

1.2. datele inițiale

2. Conversia mole fracție în masa componentei A. diagrama izobară Construcții în coordonate T # 966; A

3. Descrierea diagramei pe regiuni fuzibilitate

4. Curbele de răcire

4.1. regulă fază Gibbs

5. Determinarea masei cristalului

5.1. Concluzia regulii pârghiei

6. Ecuația Schroeder

6.1. Derivația ecuației

6.3.1. Calcularea căldurile molare de substanțe de topire A și B

6.3.2. Calcularea cristalizării incepe temperaturile componentelor A și B

6.3.3. Calcularea coeficienților de activitate ale componentelor A și B

6.3.4. Calculul cryoscopic constantele substanțelor A și B

Trimitere la proiect curs

1. Datele experimentale pentru fiecare realizare trebuie luate din tabel. „Dependența izbucnire de temperatură de cristalizare din topitură în compoziția sa (în fracțiile molare).“ Conform acestor date pentru a construi graficul izobară (T - NA).

2. Derivarea ecuația pentru a converti fracție molară în masa componentei A. Furnizați o conversie tabelară fracție molară (NA) în fracțiuni de masă (# 966; A) și de a construi diagrama izobară în coordonate T - # 966; A.

3. Descrie diagrama fuzibilitate de zonă.

4. Desenați toate tipurile de curbe de răcire (curbe în coordonate „temperatură - timp“ și le descrie, bazat pe regula de faza Gibbs).

5. ieșire ecuația pentru calcularea masei fazelor de echilibru (regula pârghiei) în zonele din grafic (T - # 966; A), în care sunt: a) cristale de componente A - se topesc; b) Componentele cristale - se topesc.

6. Se calculează masa cristalelor precipitate când răcirea topiturii 2 kg. Compoziția topiturii este dată de către profesor.

7. Derivarea ecuația Schroeder și se calculează căldura molară de fuziune a substanțelor A și B, în apropierea soluției perfecte (Nk → 1).

8. Se calculează din ecuația Schroeder, temperatura de start cristalizare a componentelor A și B din topituri de compoziție diferită. Comparați curbele experimentale de cristalizare (graficul T - NA) cu calculat.

9. Se calculează coeficienții de activitate ale componentelor A și B în soluție cu NA = 70% și NB = 67,5%.

10. La scăderea temperaturii la începutul cristalizării substanțelor A și B din compoziție soluție NA = 70% și NB = 67,5% definesc valoare constantă substanțe cryoscopic A și B, în conformitate cu datele experimentale.

Pentru a rezolva această problemă, au fost obținute următoarele date: sistem de doua componente este Li2 CO3 topit sare (Compus A) și K2 CO3 (substanța B). Aceste substanțe corespund MA masa molară = 73,89 • 10 -3 kg / mol, MW = 138 • 10 -3 kg / mol. dependența de temperatură a debutului de cristalizare a soluției din compoziția soluția prezentată în tabelul. 1.1.

O fracție molară,%

Temperatura debutului de cristalizare, K