Rata de primăvară, teorie, și calculatoare on-line

Sub influența forțelor externe ale corpului sunt în măsură să dobândească accelerația sau deformat. Deformarea este modificarea dimensiunii și (sau) forma corpului. Dacă după îndepărtarea corpului de încărcare extern restabilește dimensiunea și forma complet, atunci această deformare se numește elastică.

Lăsați primăvara în Figura 1 o forță de tracțiune îndreptată vertical în jos.

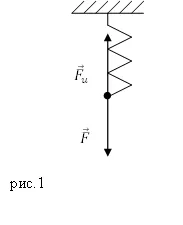
Atunci când este expusă la forța deformatoare ($ \ overline $) crește lungimea arcului. În primăvara există o forță elastică ($> _ u $), care echilibrează forța deformatoare. În cazul în care deformarea este mic și elastic, alungirea arcului ($ \ Delta l $), proporțional cu forța de denaturare:

în cazul în care ca și proporționalitatea actelor factorului de primăvară constantă $ k $. Coeficientul $ k $ este, de asemenea, cunoscut sub numele de coeficientul de elasticitate, coeficientul de rigiditate. Duritate (ca proprietate) caracterizează proprietățile elastice ale corpului supus tulpina - este capacitatea organismului de a se opune forței externe, să-și păstreze parametrii geometrici. Coeficientul de rigiditate este o caracteristică de bază de rigiditate.

constantă elastică coeficient depinde de materialul de construcție al arcului, caracteristicile sale geometrice. Astfel, constanta elastică a arcului elicoidal răsucite care este înfășurat dintr-un fir de secțiune circulară, sunt deformată elastic de-a lungul axei sale se calculează cu ajutorul formulei:

unde $ G $ modulul de forfecare (valoare depinde de materialul); $ D $ - diametrul firului; $ D_p $ - diametrul arcului elicoidal; $ N $ - numărul de bobine.

Unități de primăvară constantă

Unitatea de raport duritate în Sistemul Internațional de Unități (SI) este Newton împărțit la metru:

Coeficientul de rigiditate este egală cu forța care trebuie aplicată la primăvară pentru a modifica lungimea celalt pe unitatea de distanță.

Rigiditatea compușilor arcuri

La conectarea $ N $ compus arcuri de rigiditate se calculează folosind formula:

În cazul în care arcurile sunt conectate în paralel, rigiditatea rezultată este:

Exemple de probleme privind rigiditatea arcurilor

Sarcină. Este energia potențială ($ E_p $) sisteme de deformare a două arcuri legate în paralel, (2), în cazul în care acestea sunt egale rigiditate: $ k_1 = 1000 \ \ frac $; $ K_2 = 4,000 \ \ $ Frac, iar alungirea este \ $ Delta L = 0,01 m $.

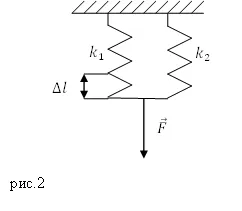
Decizie. În conexiune paralelă rigiditatea sistemului arc calculat ca:

Energia potențială a calcula deformat sistem folosind formula:

Calculăm energia potențială necesară:

Decizie. Fă un desen.

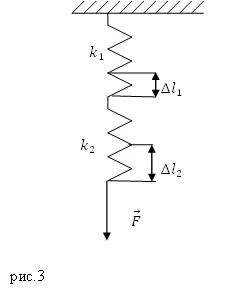
La conectarea arcuri pe fiecare dintre ele are una și aceeași forță deformante ($ \ overline $), folosind acest fapt și de drept a lui Hooke găsim prima extindere a arcului:

\ [F = k_1 \ Delta l_1 = k_2 \ Delta l_2 \ la \ Delta l_1 = \ frac \ left (2.1 \ dreapta). \]

tracțiune de lucru forța elastică a primului arc, este egal cu:

Considerand obținut în primul arc (2.1) Alungire au:

Activitatea a doua forță elastică:

Forța de muncă, care se întinde sistemul de primăvară în ansamblu, va fi găsit ca:

Substituind laturile mâna dreaptă a expresiilor (2.3) și (2.4) în (2.5), obținem: