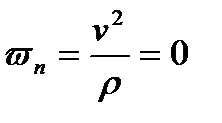1) mișcarea .Pryamolineynoe. În cazul în care punctele de cale este o linie dreaptă, atunci. atunci
și toate punctul de accelerație este egală cu o accelerație numai tangențială :. Deoarece, în acest caz, se modifică viteza de numai numeric, putem concluziona că tangenta caracterizează viteza de accelerare a schimbării valorii numerice. 2). mișcarea curbilinie uniformă. Uniforma numit o mișcare curbilinie a unui punct în care valoarea numerică a vitezei rămâne constantă în orice moment :. Apoi, tot punctul de accelerație este egală cu una numai accelerația normală:

. Vectorul accelerație este îndreptată în același timp, toate normale la traiectoria punctului. Deoarece, în acest caz, accelerația apare doar prin schimbarea direcției vitezei, putem concluziona că accelerația caracterizează viteza de schimbare de direcție. 3). mișcare uniformă. În acest caz. și, prin urmare. Rețineți că singura mișcare în care accelerația punctului este zero, în orice moment, o mișcare liniară uniformă. 4). Ravnoperemennoe mișcare curbilinie. Ravnoperemennym numit o mișcare curbilinie a unui punct în care accelerația tangențială în orice moment rămâne constantă :. Formula poate fi reprezentat sub forma integrării secundare, descoperim legea ravnoperemennogo mișcare curbilinie a unui punct dacă mișcarea curbilinie a punctului crește modulului de viteză, mișcarea se numește accelerație, și scade dacă - întârziat. Deoarece modificarea vitezei modulului se caracterizează printr-o accelerare tangențială, mișcarea va fi accelerată dacă mărimea și au același semn. În special, pentru mișcarea uniform accelerată, și dacă egalitatea. au același semn, traficul va fi accelerată în mod uniform, iar în cazul în care diferite semne - ravnozamedlennym. 5). oscilații armonice. Să considerăm mișcarea rectilinie a punctului la care distanța x de la originea O este schimbat cu timpul potrivit legii. Fluctuațiile care au loc în condițiile legii, joacă un rol important în domeniu. Ele se numesc mișcare armonică simplă. Amploarea și egală cu cea mai mare punct de deviere O din centrul de oscilație, numit amplitudinea oscilațiilor. Perioada de timp. în timpul căreia punctul efectuează o oscilație completă, numită perioada de oscilație. Determinarea accelerației proiecțiilor indică tangenta și normală (accelerația normală și tangențial) principal. Calculăm proiecții ale vectorului pe axa unui M # 964; și Mn. Deoarece vm = ds / dttoproektsiyauskoreniyanakasatelnuyu (accelerația tangențială) ______________________ Se măsoară schimbarea vitezei unui punct numai în mărime și egală cu derivata prima dată a proiecției vitezei unui punct pe direcția tangentei (din punctul de viteză algebric) sau derivata a doua a legii de mișcare a unui punct de pe traiectorie. Acum vom găsi accelerarea proiecției pe principalul normal (normalnoeuskorenie). Differentsirovanievektora T 0 neizmennoyvelichiny kuvelicheniyu conduce modul da / dt ori sale, în cazul în care, în acest caz, un - unghi de adiacenta. Înlocuirea și ___________________ _________________ ____________ obține accelerarea normală caracterizează viteza de schimbare numai în direcția. accelerație normală este egal cu raportul dintre viteza pătratul razei de curbură. accelerație normală este întotdeauna îndreptată de-a lungul principal normală la direcția de concavitate a traiectoriei (spre centrul de curbură). Extinderea pe componente de accelerare a axelor naturale obține __________________ Modul accelerare _________________ Napravlenieuskoreniyaopredelimpoformule _______________ unde μ - unghiul dintre accelerația totală și normală. Cazuri particulare ale punctului:
# 945; n = 0, # 945, # 964 = 0 - mișcare uniformă rectilinie, V = const;
# 945; n = 0, # 945; # 964; ≠ 0 - mișcarea neregulată liniară;
# 945; n ≠ 0, # 945, # 964 = 0 - mișcare curbilinie neregulată, V = const;
# 945; n ≠ 0, # 945; # 964; ≠ 0 - mișcare uniformă curbată.