Puncte de clasificare curbă plană - linie - cursul geometriei descriptive - desene, Teoria,

Tipul curbei l în apropierea unui punct M cu o singură tangentă t depinde de natura punctului de-a lungul tangentei și direcția: tangenta direcție. Să clarificăm această afirmație cu exemple.

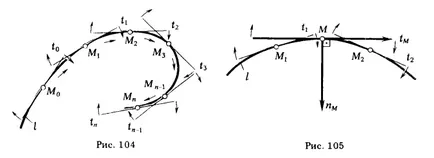
Lăsați punctul M (fig. 104) se deplasează de-a lungul curbei l. Mutarea punctului M0 (M0 ∈ l) în poziția M1 (M1 ∈ l) poate fi considerată ca deplasare a unui punct de pe arcul curbei l în direcția indicată de săgeată verde.

Prin punctul M0 și M1 tangent la curba l. Punctul M0 se poate vedea nu numai din punctul de vedere al apartenenței la curba l, dar nu și ca aparținând T0 tangenta. În acest caz, punctul de deplasare a M0 (M0 ∈ t0) în poziția M1 (M1 ∈ t1) trebuie să fie interpretată ca o mișcare pe un punct tangent în direcția indicată de săgeată verde. Și la un punct t0 ∈ M0 a luat poziția M1 ∈ T1. necesare t0 tangent tranziției la t1 poziția rotită în direcția indicată de săgeată.

La mutarea punctului M1 în poziția direcția M2 a mișcării sale de-a lungul curbei (tangent) în comparație cu o porțiune M0 M1 nu se modifică; Ea nu se schimba direcția de rotație a t1 tangenta.

Din examinarea fig. 104 arată că natura punctului de pe curba l, identificat M0 siturile M1. M1 M2. Acesta continuă și în alte părți ale M2 M3. Mn-1 Mn. Toate punctele (... M0 M1 M2 Mn) Curba l și tangentele trase prin ei (... T0 t1 t2 tn) au o proprietate comună: direcția punctului de-a lungul curbei (și tangenta) și direcția de rotație tangențială neschimbate.

Astfel de puncte și realizate prin ele sunt numite respectiv tangente la curba: ordinare (regulate) și punctul comun (obișnuit) tangential. Curve I, constând numai din puncte regulate, numită curbă lină. Fig. 105 prezintă o curbă lină și pot fi atribuite punctului regulate M s și a efectuat tangentă și normală prin aceasta la curba l.

În cazul în care direcția de mișcare a unui punct, sau de rotație a modificărilor tangente, atunci vom face cu un punct singular și tangenta specială.

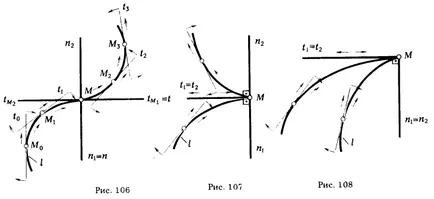
Fig. 106 prezintă curba L și indică apartenența la punctul ei M0. M1. M, M2. M3 trase prin intermediul lor t0 tangentă. t1, t, t2. t3. Vedem că, în oricare dintre aceste puncte pe direcția de deplasare a acestora de-a lungul curbei nu se schimbă. În ceea ce privește direcția tangenta de rotație, este inversat în punctul M. Acest punct este numit un punct de inflexiune. Punctele de inflexiune variază în direcția tangentei de rotație și față de curba. Cele două ramuri sunt aranjate de-a lungul unei curbe. laturile opuse ale tangentei comune t și pe partea opusă a n normale.

Fig. L prezintă o curbă de 107, cu un punct singular M, care se numește punctul de întoarcere al primului tip sau punct ascuțit. La punctele de inversare ale primului tip sunt aranjate două ramuri ale curbei pe o parte a valorii normale și pe laturile opuse ale tangenta.

Fig. 108 oferă îndrumări pe punctul de al doilea tip. * Vedem că, la punctele de inversare a doilea tip din cele două ramuri ale curbei sunt situate pe o parte a comun pentru ambele ramuri și tangenta la o parte din normal. La punctele de inversare a doilea tip nu se schimbă numai direcția de deplasare a punctului de pe curba, dar, de asemenea, direcția de rotație a tangentei.

Cu excepția cazurilor când se specifică, la punctele singulare ale curbei sunt:

a) un punct de colț (Fig. 109). In punctul de colt (este numit, de asemenea, un punct de pauză) și o direcție tangențială a modificărilor curbe la acestea „salt“ și, astfel, are o curbă la punctul M și două tangente, respectiv, două diferite normale;

* Cuspizii al doilea tip este, de asemenea, numit „cioc“.

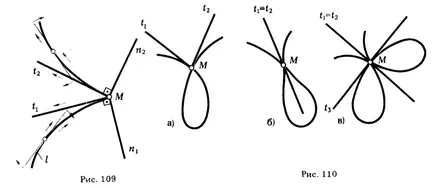
b) nod, punct sau multiplu (Fig. 110). Curba punct nodal în sine traversează. În funcție de numărul de auto-intersecții de puncte nodale pot fi: duble, triple etc. Figura ... 110 a și b sunt prezentate dublu în Fig. 110 în - punctul triplu.