produsul scalar și proprietățile sale

produs scalar nenul a doi vectori a și b este un număr egal cu produsul dintre lungimile acestor vectori de cosinusul unghiului Internat.

Notat˘a prin ab, a * b (sau (a, b)). Astfel, prin definiție,

Proprietățile produsului scalar:

1. Produsul scalar are proprietatea de comutativitate: ab = ba

5. Dacă vectorii a și b (non-zero) sunt reciproc perpendiculare, atunci produsul lor interior este zero, m. E. Dacă a ^ b, ab = 0 atunci. Reciproca deține de asemenea: dacă ab = 0 și 0 ¹ ¹b, apoi a ^ b

.

Termeni perpendiculari vector

Doi vectori nenuli sunt numite perpendiculare. dacă unghiul dintre ele este egală cu nouăzeci de grade (radiani).

Teorema: Pentru rectangularitatea doi vectori nenuli și este necesar și suficient ca produsul lor scalar este egal cu zero, și anume, că egalitatea.

Unghiul dintre vectorii

Unghiul dintre cei doi vectori. întârziat cu un singur punct, numit cel mai scurt unghiul prin care să se întoarcă unul dintre vectorii de origine la poziția de co-direcțional cu un alt vector.

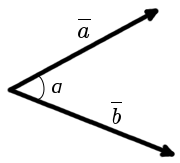
Formula de calcul a unghiului dintre vectori: