Problema podurilor din Königsberg
Referințe

Cu un titlu de noblețe „Count“ leagă tema de munca mea este doar o origine comună din cuvântul latin „Count“ - Eu scriu.

Numără ma interesat pentru abilitatea sa de a ajuta la rezolvarea o varietate de puzzle-uri. sarcini matematice și logice. Așa cum am fost pregătirea pentru Olimpiada de matematică, teoria grafurilor a fost deosebit de relevant în pregătirea mea. Am decis să aflu ce rol în fiecare zi contează joc de viață.
Scopul
Pentru a investiga rolul graficele din viața noastră.
A învăța să lucreze cu programul de formare Microsoft PowerPoint.
Aflați cum de a organiza informațiile și de a crea hyperlink-uri între slide-uri.

Ce este Earl
Cuvântul „Graficul“ în matematică înseamnă o imagine în cazul în care a pictat mai multe puncte, dintre care unele sunt conectate prin linii. În procesul de rezolvare a problemelor de matematică observat că este convenabil să reprezinte un punct de obiect. iar relația dintre cele două linii sau arce.

Ce este Earl
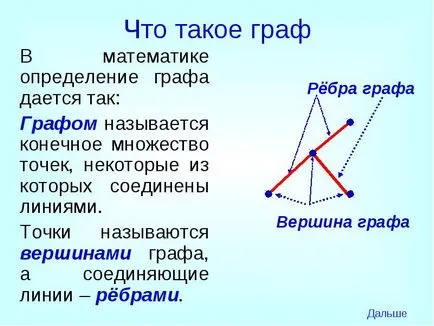
În matematică, definiția graficului este dată după cum urmează:
Contele este un set finit de puncte, dintre care unele sunt conectate prin linii.
Punctele se numesc nodurile și linii de legătură - margini.
Ce este Earl
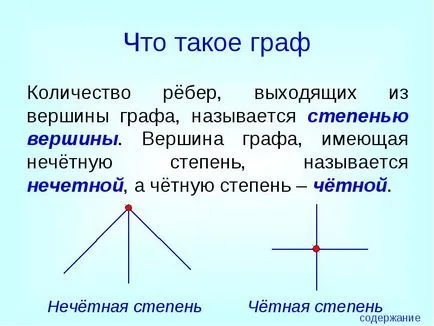
Numărul de muchii care părăsesc vârful graficului, numit gradul de vârf. Vertex având un grad ciudat, numit ciudat. și gradul chotnuyu - chiar.
Istoria graficelor de apariție
Termenul „Graficul“ mai întâi a apărut în cartea matematicianul maghiar D. Koenig în 1936, cu toate că teoreme importante inițiale pe grafice merge înapoi la Euler.

Istoria graficelor de apariție
Bazele teoriei grafic ca știință matematică stabilită în 1736, Leonhard Euler. având în vedere problema de poduri din Königsberg. Astăzi, această problemă a devenit un clasic.

Problema podurilor Koenigsberg
Fostul Königsberg (acum Kaliningrad), situat pe râul Pregelul. În oraș, râul spală cele două insule. Pe malul insulei au fost un pod. poduri vechi nu s-au păstrat, dar a existat o hartă a orașului, în cazul în care acestea sunt afișate.

Problema podurilor Koenigsberg
Kenigsbergtsy a oferit vizitatorilor următoarea problemă: să treacă pe toate podurile și a reveni la punctul de plecare. Și pe fiecare punte de legătură doar o singură dată ar trebui să viziteze.


Problema podurilor Koenigsberg
Plimbare poduri din Königsberg, respectând condițiile date, este imposibil. Trecerea de toate podurile de pe condiția de care aveți nevoie la fiecare vizită, o dată și pentru a reveni la punctul de pornire al călătoriei, în limba teoriei graficului arată ca un obiectiv de imagine „un accident vascular cerebral“ grafic.

Problema podurilor Koenigsberg
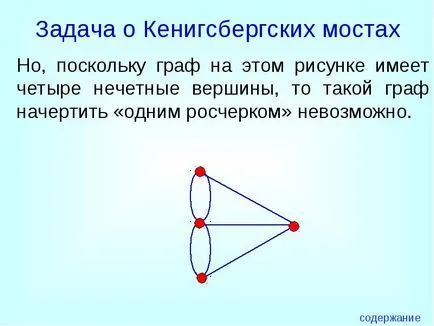
Dar, pentru că graficul din această figură are patru noduri impare, atunci un astfel de grafic desena un „un accident vascular cerebral“, este imposibil.
un accident vascular cerebral
Grafic care pot fi trase. fără a ridica creionul de hârtie, numit Euler.
Rezolvarea problemei podurilor Königsberg, Euler a formulat proprietatile graficului:
Este imposibil să elaboreze un grafic cu număr impar impar de noduri.

un accident vascular cerebral
În cazul în care toate nodurile de ciudat, puteți fără a ridica creionul de pe hârtie ( „un accident vascular cerebral“) se efectuează o singură dată, pentru a desena graficul de pe fiecare margine. Mișcarea poate începe în orice nod si termina-l în același top.

un accident vascular cerebral
Un grafic care are doar două noduri impare. Acesta poate fi trasă fără a ridica creionul de hârtie, iar mișcarea trebuie să înceapă cu una dintre aceste vârfuri ciudate și să termin în a doua dintre ele.
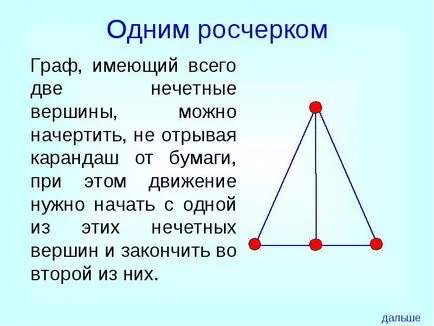
un accident vascular cerebral
Un grafic care are mai mult de două noduri ciudat, este imposibil de a trage o „un accident vascular cerebral“.
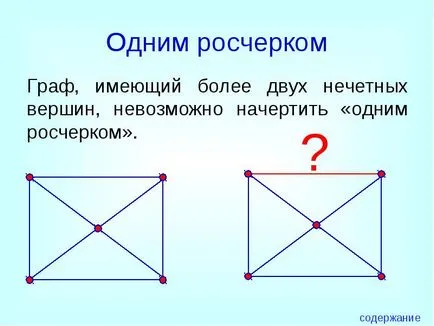
Utilizarea graficelor
Cu ajutorul graficelor simplificate de rezolvare a problemelor matematice, puzzle-uri. sarcini dificil.
Utilizarea graficelor
Arkady și Boris. Vladimir, Grigore și Dimitri la întâlnire schimbate strângeri de mână (fiecare dat mâna cu fiecare la un moment dat). Câte strângeri de mână au fost făcute?

Utilizarea graficelor
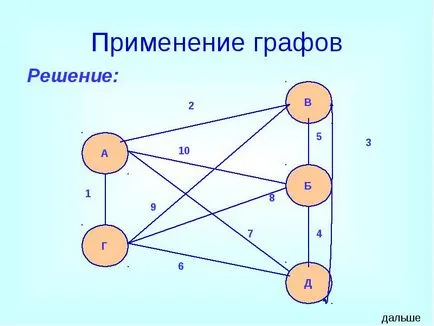
Utilizarea graficelor
Labirintul - un grafic. Și exploreze - este de a găsi o cale în acest grafic.
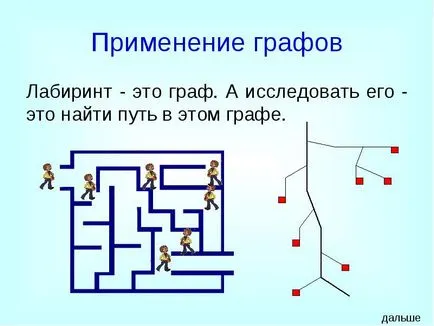
Utilizarea graficelor
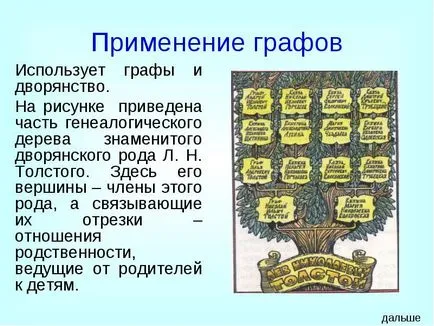
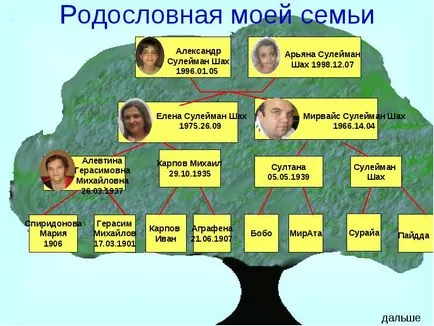
Acesta utilizează grafice și nobilimii.
Figura prezintă o parte din arborele genealogic al faimoasei familii nobile L. N. Tolstogo. Aici, partea sa superioară - membrii acestui gen, și care leagă segmentele lor - relații de afinitate care duce la părinți la copii.
Utilizarea graficelor
Grafitul este un bloc - circuite de programare pentru calculatoare.
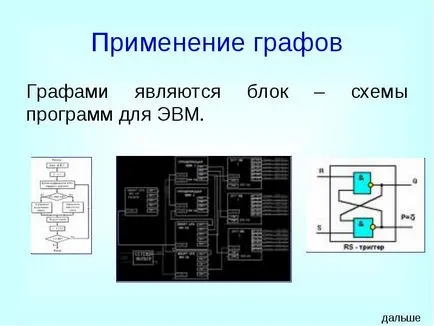
Utilizarea graficelor
Grafitul este programele de construcție de rețea.
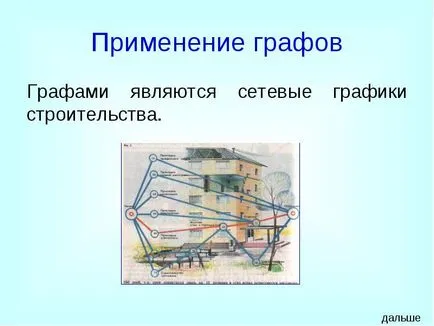
Utilizarea graficelor
- grafice tipice pe hărți sunt imaginea căilor ferate.

Utilizarea graficelor
- grafice tipice pe hărțile ale orașului sunt modelele de trafic de transport urban.
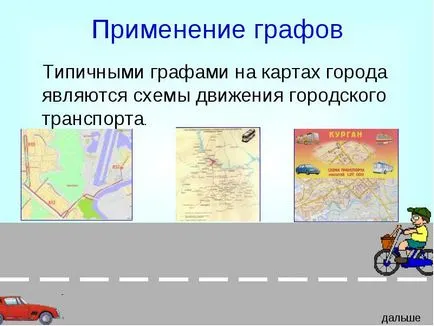
Utilizarea graficelor
grafice tipice sunt scheme ale liniilor aeriene, care sunt adesea afișate la aeroporturi.
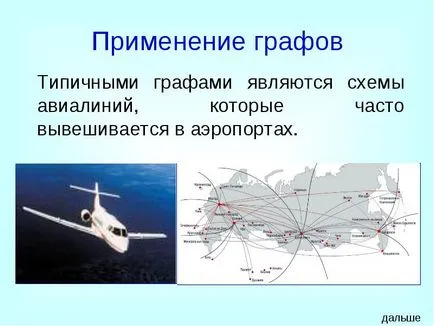
Utilizarea graficelor

Utilizarea graficelor
Contele este sistemul de străzi ale orașului. Sale de top - piețe și intersecții, și marginile - pe străzi.

Utilizarea graficelor

Utilizarea graficelor
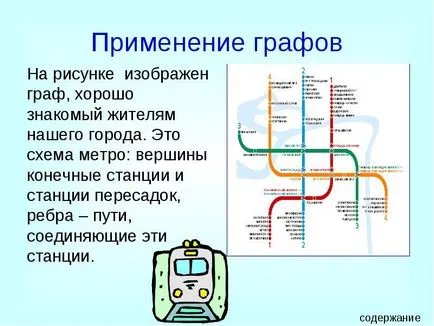
Figura prezintă un grafic, familiar locuitorii din orașul nostru. Această schemă de metrou: la stațiile de capăt și stații directe, coaste - rute care leagă aceste stații.
Graficele - un remarcabil obiecte matematice, cu ajutorul căruia se poate rezolva probleme matematice, economice și logice. Puteți rezolva, de asemenea, diverse puzzle-uri și de a simplifica condițiile de probleme în fizică, chimie, electronica si automatizari. Graficele sunt folosite în prepararea de hărți și arbori de familie.
În matematică, există chiar și o secțiune specială, care se numește „teoria Graph“.

Referințe
3.Grafy și aplicarea lor, O. Ore, București, 1979.
