pătrate Magic de piese de domino

Fig. 7 prezintă un pătrat de 18 oase de domino, fapt remarcabil că suma punctelor din fiecare din seria - longitudinală, laterală și diagonală - și unul

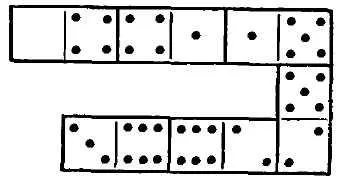
Aceleași 13. Aceste piețe au fost mult timp numit „magic“.

Sunteți invitat să facă mai multe din aceleasi 18-piatra pătrate magice, dar cu o sumă diferită de puncte într-un rând. 13 - cea mai mică valoare în rândurile pătrat magie, formate din 18 de oase. Cea mai mare sumă - 23.

Progresia piese de domino.

Puteți vedea în Fig. 8 șase oase piese de domino stabilite în conformitate cu regulile jocului și se caracterizează prin aceea că numărul de puncte de pe oase (în cele două jumătăți ale fiecărui os) este crescut cu 1 Seria începe cu 4 și constă din următorul număr de puncte:

O astfel de serie de numere care crește (sau descrește) într-una și aceeași valoare se numește „progresie aritmetică“. În seria noastră, fiecare număr este mai mare decât cel precedent de unul; dar progresia bolii poate fi orice alt „diferență.“

Provocarea este de a face câteva progresii 6-piatră.

JOC DE 15 SAU Luate

Cutie proverbial cu 15 piese pătrate numerotate are o istorie curios că puțini jucători știu despre. Ne spune despre cuvintele ei germană jocuri cercetător, matematica W. Arens.

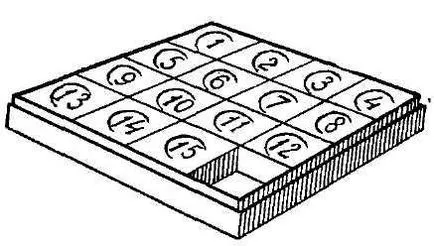
Fig. 9. Jocul de 15.

„Aproximativ o jumătate de secol în urmă - la sfârșitul anilor '70 - a apărut în Statele Unite ale Americii,“ jocul de 15“, sa răspândit repede și, datorită nenumărate numere de jucători, ea a captivat, a devenit un dezastru social real.

„Același lucru a fost observat pe această parte a oceanului, în Europa. Ar putea chiar Conca pentru a vedea în mâinile cutii pasagerilor cu 15 piese. Birouri și magazine proprietarii disperați de entuziasm angajaților săi și a trebuit să le interzică să se joace în orele de studiu și comerț facilități de divertisment. Proprietarii utilizate inteligent mania și pus în scenă turnee mari de jocuri de noroc.

Jocul a pătruns chiar și în sălile solemne ale Reichstag-ului german. „Eu pot vedea în continuare oameni cu părul cărunt, în Reichstag, având în vedere concentrat în mâinile lor o cutie pătrat“ - amintește celebrul geograf și matematician Zigmund Gyunter, fost adjunct în timpul unei epidemii de jocuri de noroc.

„În 1880, jocurile de noroc a ajuns la o febra, se pare, cel mai înalt punct, dar la scurt timp după aceea tiranul a fost învins, și a învins matematicieni arme teoria jocurilor matematice a constatat că multe dintre sarcinile care pot fi oferite, rezolvabile doar jumătate; .. Celălalt nu este solubil fără trucuri.

„A devenit clar de ce anumite sarcini nu a răspuns la eforturile cele mai persistente, și de ce organizatorii turneului a îndrăznit să numească o primă uriașă pentru soluționarea problemelor. În acest sens, a depășit toate jocurile inventator, care a oferit editorul ziarului New York

supliment de duminică prost la o primă de 1.000 $ pentru rezoluția sa; ca editor ezitat, inventatorul și-a exprimat disponibilitatea de a se face o sumă pe nume din propriul său buzunar. Numele inventatorului Samuel (Sam) Loyd. El a devenit cunoscut ca un compozitor de sarcini plin de duh și o varietate de puzzle-uri. Este interesant faptul că, în America de a obține un brevet pentru un joc inventat de el nu a reușit. Conform instrucțiunilor, el a trebuit să prezinte un „model de lucru“ pentru executarea lotului de testare; el a oferit ofițerul sarcina oficiului de brevete, iar atunci când acesta din urmă a întrebat, dacă este solvabilă, inventatorul a trebuit să răspundă: „Nu, e matematic imposibil“ „În acest caz, - urmată de o obiecție - nu poate fi un model de lucru, și nici un model și nici un brevet.“ Loyd a fost mulțumit cu această rezoluție - dar, probabil, ar fi fost mai persistente, dacă sunt prevăzute succesul fără precedent al invenției sale „[Acest episod folosit de Mark Twain în romanul său.“ Challenger american „.]

Aici este povestea lui proprie inventatorului jocului unora dintre faptele istoriei sale:

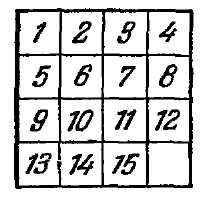
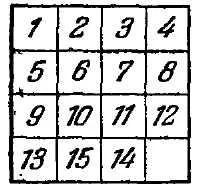
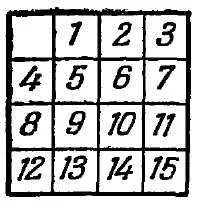
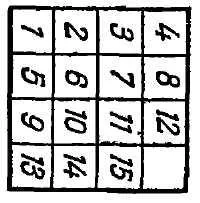
„Rezidenții pe termen lung în timp ale regatului de spirit, - spune Loyd, - amintiți-vă cum la începutul anilor '70, am făcut întreaga lume pentru a puzzle-ului într-o cutie cu mutarea piesele, a devenit cunoscut sub numele de“ joc 15 „(Figura 10) Cincisprezece proiecte au fost.. aranjate într-o casetă pătrată în ordinea corectă, și numai piesele 14 și 15 au fost rearanjate așa cum se arată în figură însoțitoare (Fig. 11). obiectivul a fost secvențial în mișcare dame, pentru a le aduce în poziția lor normală, în care, cu toate acestea, ordinea blocurile 14 și 15 trebuie corectate.

„Premiul de 1.000 $ oferit pentru prima soluție corectă pentru această problemă, nimeni nu a fost meritat, deși a rezolvat neobosit această problemă. Ei au spus povești amuzante despre comercianți, uitați din cauza acestei deschise magazinele lor, pe venerabilii oficiali, toată noaptea este inactiv . sub un felinar, căutând o cale de a rezolva nimeni nu a vrut să renunțe la căutarea unei soluții, pentru că toate simțit încrezător în navigatoare lor de succes de așteptare, să zicem, din cauza jocului au fost puse pe navele lor eșuare, mașiniști a fost realizată de către stațiile de tren. agricultori Au aruncat pluguri lor. "

Vom introduce cititorul la rudimentele teoriei jocului. În forma sa completă este foarte complexă și este strâns legată de unul dintre departamentele de Algebra ( „teoria determinanților“). Ne limităm doar la unele dintre considerațiile expuse B. Ahrens.

„Sarcina jocului este de obicei prin mișcări succesive permise de prezența transferului câmp liber orice locație inițială de 15 stick-uri la normal, adică una în care bombe sunt în ordinea numerelor lor: .. din stânga sus colțul din 1, dreapta .. - 2, apoi 3, apoi în colțul din dreapta sus 4, în următoarea ordine de la stânga la dreapta: 5, 6, 7, 8, etc. Aceasta este locația finală normală prezentăm aici în figura 10 ..

„Imaginați-vă acum locația în care 15 blocuri sunt situate în mizerie colorate. Aproape de mișcare poate fi întotdeauna adusă la Verificator 1 locul pe care îl ocupă în figură.

. „Este de asemenea posibil, fără a atinge Checkers 1 plumb bombă 2 pe un loc adiacent la dreapta, apoi, fără a atinge blocurile 1 și 2, pot fi plasate Checkers 3 și 4 naih locul obișnuit dacă se întâmplă să găsească în ultimele două rânduri verticale, apoi duce cu ușurință în această regiune și apoi mișcarea următoare pentru a obține rezultatul dorit. acum, linia de sus 1, 2, 3, 4 este prevăzută în ordine, și manipularea în continuare a piesele pe care le atingem acest număr nu va. în același mod a încercat să punem în ordine și un al doilea line: 5, 6, 7, 8, este ușor de văzut că atinge întotdeauna . Gibly Mai mult, în ultimele două rânduri ale spațiului trebuie să fie adus la dame poziția normală 9 și 13, de asemenea, este întotdeauna posibil, toate enumerate în ordinea blocurilor 1, 2, 3, 4,5,6,7,8,9 și 13 în continuare. audio nu sunt mutate ;. rămâne mică întindere de șase domenii, în care unul este liber, iar celelalte cinci sunt ocupate de dame 10, 11, 12, 14, 15 la întâmplare în această porțiune de șase scaun poate fi adus întotdeauna în verificatoare spațiu normale 10, 11 12. Atunci când se ajunge, ultimul rând de dame 14 și 15 vor fi situate fie în ordinea normală Sau în sens invers (Fig. 11). Într-un mod care cititorii pot verifica cu ușurință în această privință, avem următorul rezultat.

„Orice poziție inițială poate fi adusă la locația sau Fig. 10 (poziția I) sau Fig. 11 (poziția II).

„Dacă o locație, care, pentru concizie notate cu litera S. poate fi transformată într-o poziție I, atunci, în mod evident, opusul este posibil - pentru a traduce poziția I în poziția S. După toate mișcările de dame sunt reversibile: dacă, de exemplu, în Schema I, putem bombarda 12 plasate pe un câmp liber, este posibil să se deplaseze acest lucru imediat relua mișcarea opusă.

„Deci, avem doua astfel de aranjament serie care dispozițiile unei serii pot fi convertite la I normale, iar cealaltă serie -. În poziția II și invers, de la locația normală, puteți obține orice poziție din prima serie, și de la locația II - orice poziție de-a doua serii. în cele din urmă, oricare două locații aparținând aceleiași serii, pot fi transformați unul în altul.

? „Este posibil să meargă mai departe și să combine cele două locații - I și II pot fi dovedită riguros (nu vom intra în detalii) că dispozițiile acestea nu se transformă una în cealaltă, în orice număr de mișcări este motivul pentru care toate numărul mare de piese de plasare este împărțit în două serii disparat :. 1) cele care pot fi convertite într-un i normal: este - poziția solubila, 2) cele care pot fi convertite în poziția II și, prin urmare, în niciun caz, să fie transferată la locația normală: ea - dispoziții care să permită care naznachalis s bonusuri uriașe.

„De unde știi dacă locația specificată aparține prima sau a doua serie? Un exemplu va clarifica acest lucru.

„Considerăm că un astfel de aranjament.

. „Primul rând de blocuri, în ordine, ca al doilea, cu excepția ultimelor dame (9) Acest bloc are loc, care în locația normală aparține 8.Shashka 9 ar trebui, prin urmare, raneeshashki 8: este ordinea normală de preemțiune menționată ca“ o mizerie „Oh. Verificator 9, spunem: aici este o tulburare de loc 1 considerând Checkers suplimentare găsi „anticipare“ pentru dame 14, acesta este plasat pe trei locații (blocuri 12, 13, 11), înainte de poziția sa normală, aici avem 3 tulburare (14, anterior 12. , 14 mai devreme 13 ;. 14, anterior 11) Total am numărat 1 + 3 = 4 tulburare în plus, br. Ashka 12 dame plasate anterior 11, și în mod similar, blocul 13 Checkers anterior 11. Acest lucru oferă încă 2 tulburare. Total au 6 tulburări. În mod similar, pentru fiecare locație stabilit numărul total de tulburări, pre eliberând ultimul loc în colțul din dreapta jos. Dacă numărul total tulburări ca și în cazul de mai sus, chiar, locația predeterminată poate fi adus la un capăt normală, cu alte cuvinte, ea aparține solubil. Dacă numărul de inversiuni este impar, locația aparține a doua serie, t. E. (presupusă a fi un număr par de revolte nule) la insolubile.

„Cu claritate, a introdus acest joc în matematică, fosta pasiune febrilă în hobby este acum de neconceput. Matematica a creat o teorie cuprinzătoare a jocului, teoria nu lasă nici un punct îndoielnice. Rezultatul jocului nu depinde de nici o șansă, nu de resurse, atât în alte jocuri, dar dintr-o factori pur matematic care o determină cu certitudine absolută. "

Să ne întoarcem acum la puzzle-uri în acest domeniu.

Iată câteva probleme rezolvabile, inventate de inventatorul jocului:

Prima sarcină Lloyd.

Pe baza aranjamentul prezentat în Fig. 11, plumb dame în ordinea corectă, dar cu un câmp liber în colțul din stânga sus (fig. 13).

Cea de a doua sarcină Lloyd.

Bazat pe localizarea Fig. 11 Întoarceți caseta de un sfert de tură și pentru a muta piesele, atâta timp cât acestea nu iau aspect Fig. 14.

A treia sarcină Lloyd.

Mutarea piesele în conformitate cu regulile jocului din poziția din fig. 11, rândul său, caseta din „pătrat magic“, și anume, loc șubredă, astfel încât suma numerelor a fost în toate direcțiile este de 30.

Prinderea puzzle-uri legate de jocul de domino și 15, am stat în termen de aritmetică. Revenind la puzzle-ului pe terenul de crochet, am ajuns parțial în geometrie.

Propun următoarele cinci sarcini jucători crochet.