Operațiuni cu vectori și matrici

Matricele sunt cele mai populare obiecte de sistem MATLAB, care este special conceput pentru a efectua calcule complexe cu vectori, matrice, și matrice. O importanță deosebită este atașat matrici 1x1. care sunt scalari si matrici având o singură coloană sau un singur rând, - vectori.

Luați în considerare moduri de a construi matrici. În exemplele care urmează un vector coloană este o matrice de dimensiune 3x1. vector rând este o matrice de dimensiune 1x3. scalar și matrice 1x1:

Sarcina matrice necesită câteva rânduri. Fiecare linie se termină cu punct și virgulă. Astfel, intrarea

specifică matricea pătrată, care pot fi afișate prin tastarea în linia de comandă M și apăsând Enter:

Deoarece elementele de matrice pot fi utilizate expresii aritmetice, de exemplu:

Pentru a specifica un singur element al matricei utilizat indici. Elementul din rândul I și coloana J a matricei A este notat cu A (I. J). Dacă elementul A (. 02 martie), trebuie să se atribuie o valoare de 10, introduceți comanda:

Exprimarea M (I), cu un singur indice permite accesul la elementele de matrice desfășurate într-o singură coloană. În acest caz, matricea este considerat ca un vector lung format din coloanele matricei originale. Astfel, pentru exemplul discutat anterior cu matricea M. M (4) - este o altă modalitate de a se referi la valoarea 2 este stocată în M (1 luna februarie.).

Dacă încercați să utilizați valoarea unui element din afara matricei, MATLAB va genera o eroare:

. Indicele depășește dimensiunile matricei.

Cu toate acestea, în cazul în care matricea elementului cu indici mai mari decât dimensiunea sa, atribuie o anumită valoare, dimensiunea creșterii matricei, de exemplu:

Colon - acesta este unul dintre cei mai importanți operatori MATLAB. Acesta este utilizat într-o varietate de expresii. Pentru a crea un vector rând cu componente întregi 1 până la 10 suficientă pentru a executa comanda:

1 2 3 4 5 6 7 8 9 10

Pentru intervalul de retur, vom introduce creștere:

93 86 79 100 72 65 58 51

0 0,7854 1,5708 2,3562 3,1416

Operator „colon“ este folosit pentru a forma submatricile și subvectors ale vectorilor, matricelor și matrici multidimensionale:

· M (:) înregistrează toate elementele de matrice M ca o coloană.

Din exemplul de mai sus rezultă că vectorii pot fi utilizate ca indici. Dacă vectorii V și X, X (V) poate fi reprezentat ca un vector [X (V (1)). X (V (2)), ..., X (V (n))]. Elementele vectorului V trebuie să fie întregi, astfel încât acestea să poată fi utilizate ca indici ai elementelor X. matrice O eroare este emisă atunci când indicele este mai mică decât unitatea sau mai mare decât dimensiunea (X). Același principiu este valabil pentru indicele matricelor. Dacă vectorul V m are o componentă, iar vectorul W - (. V W) n componente, atunci M este dimensiunea matricei MXN. formate din elemente ale matricei codurilor M. care - elementele vectorilor V și W.

Indicii Vector pot fi utilizate în operațiuni de atribuire, cum ar fi:

M (I. J) = B B atribuie valori elementelor matrice submatrice dreptunghiular M. vectori definiți I și J. matrice B ar trebui să aibă o lungime (I) de rânduri și coloane de lungime (J). Următorul exemplu este utilizat pentru a indexa un vector de permutare coloanele 2 și 3 din matricea B. Rezultatul este plasat în matricea A:

Ștergerea rânduri și coloane.

Rânduri și coloane ale matricei pot fi îndepărtate utilizând paranteze pătrate goale [].

Crearea unei matrice de dimensiune 4x4 magie:

Apoi îndepărtați a doua coloană:

Folosind un index în loc de două sau indicele vector poate fi îndepărtat din matricea unuia sau mai multor elemente de probă, respectiv. Când această matrice este transformată în vectorul rând:

Combinând matrice - procesul de conectare a unui număr de matrici într-o singură mare. De fapt, matricea inițială este generată prin combinarea elementelor sale individuale. Operatorul Union - o pereche de paranteze pătrate. Astfel, [A, B] - concatenare orizontală (asociație) a matricelor A și B. care trebuie să aibă același număr de rânduri. Concatenare orizontală poate fi aplicat la orice număr de matrici din una paranteze: [A, B, C]. Când matricea verticală concatenarea în paranteze pătrate separate prin virgulă: [A; B; C]. concatenare orizontală și verticală pot fi utilizate simultan.

Matricele pot fi transpuse prin intermediul operatorului „(apostrof), de exemplu, A“ - transpusa matrice A. Pentru matrici complexe transpun suplimentate de conjugare complexă. Linia a matricei transpuse corespund coloanelor matricei originale.

Crearea de matrici cu proprietăți dorite.

Pentru a crea o matrice identitate servește ca funcție de ochi:

· Ochi (n) - returnează matricea identitate de dimensiune nxn;

· Ochi (. M n) - returnează matricea mxn dimensiune cu cele de pe diagonala;

· Eye (mărimea (A)) - returnează matricea identitate de aceeași mărime ca A.

Un exemplu de utilizare a funcției ochilor:

Pentru a crea o matrice, toate elementele care - unitatea utilizată funcția altele:

· Ones (n) - returnează matricea dimensiune nxn. toate elementele care - unitatea;

· Ones (m, n) - returnează matricea dimensiune mxn. constând din unități;

· Ones (dimensiune (A)) - returnează o matrice de unități de aceeași dimensiune ca și A.

Crearea unei matrice de zero oferă o zerouri de funcții. ale cărui argumente sunt aceleași ca și cele din funcția.

Crearea unei matrice cu elemente diagonale specificate permite diag funcția:

· X = diag (v, k). - pentru vectorul v constând în n component X returnează o matrice pătrată de ordinul n + abs (k), cu elemente de pe k diagonala v th la k = 0 este diagonala principală, cu k> 0 - cel superior al diagonalelor, cu k <0 – одна из нижних диагоналей. Остальные элементы матрицы – нули;

· X = diag (v) - pune vectorul v pe diagonala principală;

· V = diag (. X k) - pentru matricea X returnează un vector coloană care constă din elementele X matrice k -lea diagonală;

· V = diag (X) - returnează diagonala principală a matricei X.

Pentru a crea o matrice compusă din alte matrici, servesc următoarele funcții:

· Repmat (. A [m n p ...]) returnează o matrice multidimensionale constând din copii ale matricei A. Matricea A poate fi multidimensională;

· Repmat (a. M, n) returnează o matrice de elemente MXN dimensiuni cu valori date cu un scalar a.

Funcția linspace generează un șir liniar de noduri echidistante. Formulare de cerere:

· Linspace (a, b) care formează o matrice liniară de 100 de puncte distribuite uniform pe intervalul de la a la b;

1,0 1,2500 1,5000 1,7500 2,0000

Crearea unui vector de puncte la distanțe egale pe o scară logaritmică.

Funcția logspace generează un vector de puncte la distanțe egale pe o scară logaritmică. Formulare de cerere:

· Logspace (a, b) formează vectorul rând de 50 de puncte la distanțe egale pe o scară logaritmică între decenii 10 a și 10 b;

Toate funcția argumente logspace trebuie să fie valori scalare.

Matricea care conține un număr mare de elemente cu valori zero, numite rare. Aceste matrici sunt, de obicei apar la rezolvarea problemelor la limita pentru ecuații diferențiale prin sisteme mesh. Cu matrici rare este convenabil să funcționeze, folosind schema de stocare compactă doar elemente nenule ale matricei. În plus față de elementele de bază non-zero, într-un format rar necesar pentru informații de index magazin care indică locația fiecărui element într-o matrice regulat. Aceste informații suplimentare este prețul pe care trebuie să plătească pentru refuzul de depozitare la zero. Pentru matrici rare în MATLAB are un număr de funcții, o selecție de care este prezentată mai jos:

· [B. d] = spdiags (A) B. creează o matrice rară ale cărei coloane sunt nenul matrice A. diagonală Vectorul d conține numerele de diagonalelor nenule;

(. A d) · B = spdiags B. creează o matrice rară ale cărei coloane sunt în diagonală nenul matrice A. anumit vector d;

· Full (S) convertește S matrice rară în totalitate;

· S = rare (A) convertește matrice rară completă;

· S = rare (i. J. S. M. N) creează o matrice rară S dimensiune mxn. Vectorii i și j definesc pozițiile și elementele sunt parte integrantă, și vectorul s determină o valoare număr real sau complex al elementului de matrice. Vectori i. j și s trebuie să aibă aceeași lungime.

Noi construim sistemul de ecuații matrice, care apare atunci când aproximarea derivatei a doua noduri pe o grilă uniformă:

Lista de ieșire conține elemente nenule ale matricei S, împreună cu indicii de rânduri și coloane. Toate elementele sunt sortate după coloană. matricea S sparse din acest exemplu pot fi create în mod direct, fără conversie:

MATLAB are o gamă largă de instrumente grafice, variind de la comenzi simple pentru construirea graficelor de funcții de o variabilă și terminând cu grafica combinate și de prezentare cu elemente de animație, precum și mijloace de proiectare a unui interfață grafică cu utilizatorul (GUI). O atenție deosebită este acordată sistemului de grafice tridimensionale cu figuri funcționale afișaj color și imitație de diferite efecte de iluminare.

comanda complot are diferite forme asociate cu parametrii de intrare, de exemplu, plot (y) produce un grafic liniar al componentelor pe porțiuni vectoriale y ale indicilor lor. Dacă cei doi vectori sunt stabilite ca argumente, plot (x, y) creează un grafic y din x. De exemplu, pentru a construi graficul sin (x) în intervalul de la 0 la 2p. este necesar să-și îndeplinească toate cele trei echipe:

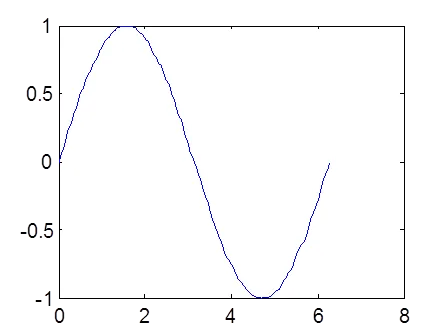
complot apel funcții cu mai multe perechi x-y crea mai multe curbe pe același grafic. MATLAB atribuie automat fiecare curbă de culoare (în cazul în care nu o fac eu). În plus față de vectorul y pentru a construi două seturi de date și derivă toate cele trei curbe pe același grafic:

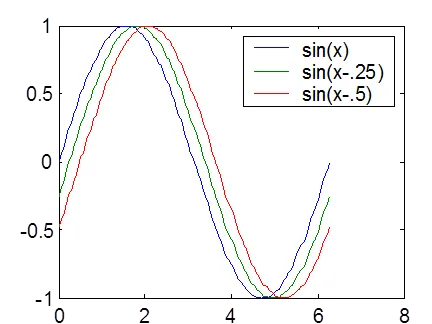
puteți utiliza legenda de comandă pentru a identifica fiecare curbă: