Numărul pitagoreice 1967 Perelman I

numere pitagoreice

User-friendly și metoda foarte precise utilizate pentru topografilor pe liniile perpendiculare la sol, este după cum urmează. Să prin punctul A este necesară pentru linia MN perpendicular (Fig. 13). Un laic în direcția AM de trei ori pe zi și la distanță. Apoi, fixați cablul de trei noduri, distanțele dintre ele sunt egale cu 4a și 5a. Punerea noduri extreme la punctele A și B, trageți cablul de nodul de mijloc. Cablu situat triunghi, în care unghiul A - trăi.

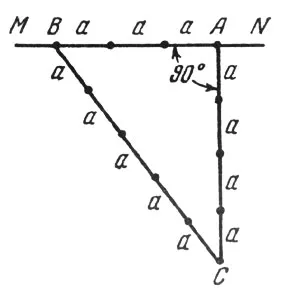
Fig. 13. Să presupunem că, prin punctul A este obligat să efectueze o linie perpendiculară MN

Această metodă veche se pare că se aplică acum chiar milenii, constructorii piramidelor egiptene, bazate pe faptul că fiecare triunghi ale cărui laturi sunt în raportul 3: 4: 5, în conformitate cu bine-cunoscut teorema lui Pitagora - dreptunghiular, așa cum

In plus numerele 3, 4, 5, sunt cunoscute nenumărate numere naturale a, b, c, care satisfac relația

Acestea se numesc numere pitagoreice. Conform teoremei lui Pitagora, aceste numere pot fi lungimile laturilor unui triunghi dreptunghic; astfel încât a și b sunt denumite „picioare“, și cu - „ipotenuzei“.

Este clar că, în cazul în care a, b, c este un număr triplu pitagoreice și Pa, Pb, Pc, unde p - un multiplicator întreg - numere pitagoreice. Pe de altă parte, în cazul în care numerele pitagoreice au un factor comun, atunci acest lucru poate fi un factor comun toate tăiate, și din nou se va tripla numere pitagoreice. Prin urmare, vom explora mai întâi un trio de numere pitagoreice relativ prime (restul sunt obținute din acestea prin înmulțire cu un factor întreg p).

Ne arată că, în fiecare dintre aceste triplete și, b, c unuia „picioarele“ ar trebui să fie chiar și celălalt inegală. Să vorbim „contrariul.“ În cazul în care atât un „picior“ și b sunt chiar, numărul este chiar un 2 + b 2. o medie și „ipotenuză“. Aceasta, cu toate acestea, contrazice faptul că numerele a, b, c nu au factori comuni, deoarece cele trei numere chiar au un factor comun 2. Astfel, cel puțin unul dintre „picioare“ a, b este impar.

Rămâne o altă posibilitate: a „picior“ două „ipotenuză“ ciudat și chiar. Nu este dificil de a dovedi că nu poate fi. Într-adevăr, dacă „picioarele“ au forma

atunci suma pătratelor lor este egală cu

t. e. este un număr care atunci când este împărțit la 4 dă un rest de 2. pătrat În același timp fiecare număr chiar trebuie să fie împărțit la 4 fără rest. Prin urmare, suma pătratelor a două numere impare nu poate fi un pătrat al unui număr par; cu alte cuvinte, cele trei numere - nu pitagoreice.

Deci, de la „picioare“ a, b, unul este chiar și celălalt ciudat. Prin urmare, numărul de 2 + b 2 este impar, de aceea, ciudat și „ipotenuză“ cu.

Presupunem pentru definiteness că este ciudat „picior“, la fel de bine, și chiar și-b. egalității

obținem cu ușurință:

Multiplicatoare c + b și a - b, în partea dreaptă, sunt relativ prim. Într-adevăr, în cazul în care aceste numere au un prim factor comun, altele decât unitatea, atunci acest factor ar fi împărțit și suma

t. e. numărul 2c, 2b, și ar avea un factor comun. Din moment ce un este ciudat, atunci acest factor este diferit de doi, și pentru că la fel au factorul comun al numărului a, b, c, care, cu toate acestea, nu poate fi. Această contradicție arată că numerele cu + b și a - b sunt relativ prim.

Dar, în cazul în care produsul a unui număr relativ prime este un pătrat perfect, fiecare dintre care este un pătrat, t. E.

Rezolvarea acestui sistem, vom găsi:

Numerele pitagoreice Deci vizualizate sunt de forma

unde m și n - unele numere impare relativ prime. Cititorul poate verifica cu ușurință și invers: pentru orice tip impar formulă pitagoreic scris dat trei numere a, b, c.

Iată câteva numere de triplete pitagoreice obținute la diferite tipuri:

(Toate celelalte numere pitagoreice triple sau au un factor comun, sau să conțină un număr mai mare de o sută.)

Numerele pitagoreice au, în general, o serie de caracteristici interesante, pe care le indicați mai jos, fără dovezi:

Unul dintre „picioarele“ trebuie să fie divizibil cu trei.
Unul dintre „picioarele“ trebuie să fie un multiplu de patru.
Unul dintre numerele pitagoreice trebuie să fie un multiplu de cinci.

Cititorul poate verifica existența acestor proprietăți, vizualizarea exemplele de mai sus ale grupurilor de numere pitagoreice.