Număr fuzzy 4

4.1 Conceptul de număr neclare

Număr fuzzy - aceste variabile fuzzy, pe axa reală, cu alte cuvinte, numărul neclare este definit ca mulțimea fuzzy

pe platourile de filmare de numere reale o funcție de membru , unde .

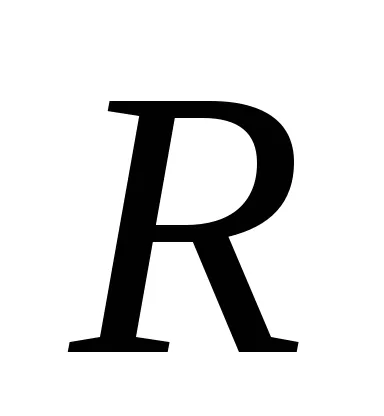
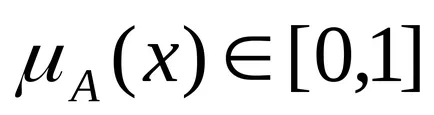
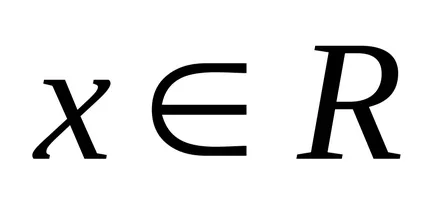
Numărul Fuzzy este numit normal. dacă este convexă. dacă pentru orice

efectuat

.

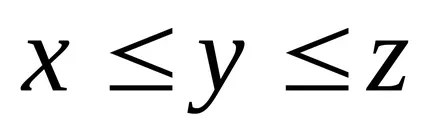
multe

- Număr neclare nivel Acesta este definit ca un set clar de

.

subgrup

Acesta a solicitat sprijinul numărului neclare , dacă

.

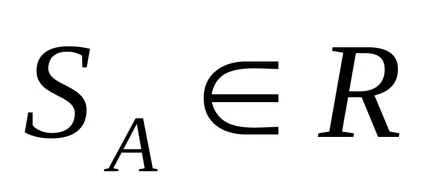
Număr neclare unimodale. în cazul în care condiția

Este valabil numai pentru un singur punct al axei reale.

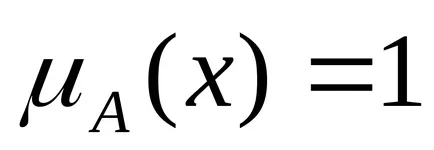
Numărul neclară Convex se numește zero, dacă este neclară

.

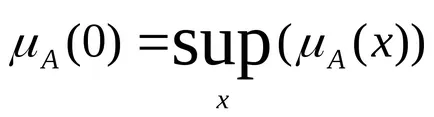
Numărul fuzzy este pozitiv. dacă

și negativ. dacă .

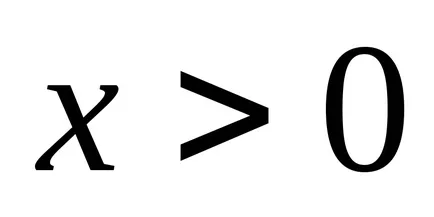
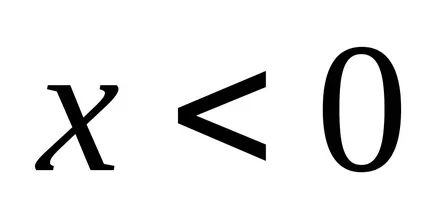
4.2 Operații cu numere fuzzy,

Extinse operații aritmetice binare (. Adunare, înmulțire etc.) pentru numerele fuzzy, se determină prin operații adecvate pentru a șterge numere folosind o generalizare a principiului după cum urmează:

Utilizați operații algebrice astfel definite pe numere fuzzy este inutilizabil din cauza cantității mari de calcul. Deci, este adesea folosit în reprezentarea numerelor fuzzy,

- formă care se potrivește cu descrierea din stânga (stânga) și (dreapta), părțile din dreapta ale funcției de membru.

Număr fuzzy

- Formularul are o idee

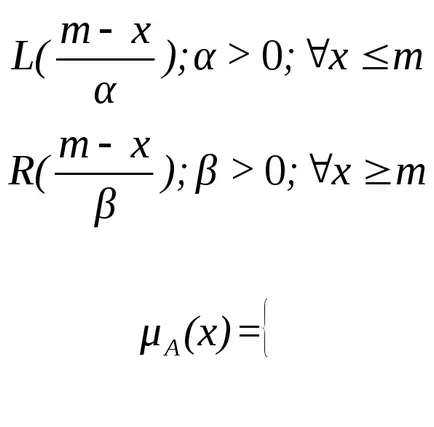
unde

și - funcții au următoarele proprietăți:

,

.

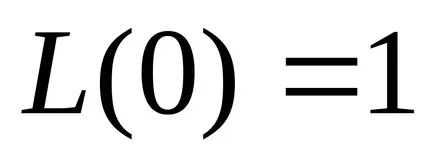
funcție

scade monoton în intervalul . aici - valoarea medie a unui număr de neclare, - abatere de la valorile medii din stânga, - Deformarea dreapta. dacă == 0, atunci numărul de neclar Se merge într-un număr clar .

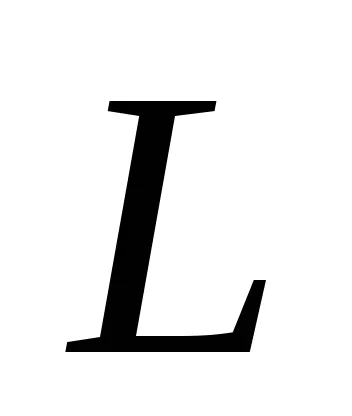
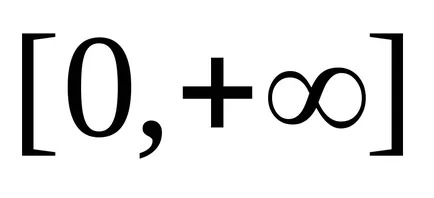
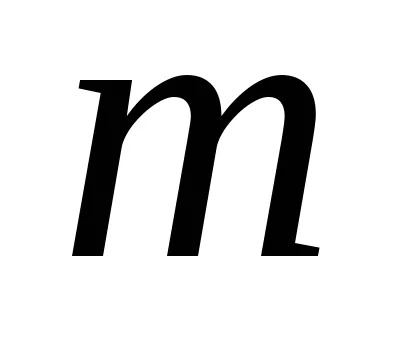
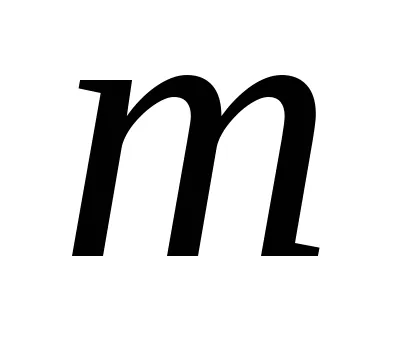
Astfel, un număr de neclare

- forma poate fi reprezentat ca triplete. Apoi, operații aritmetice cu numere fuzzy, pot fi determinate prin operarea treiari lor respective:

în practică

- Reprezentarea este simplificată prin utilizarea funcțiilor liniare, ceea ce conduce la un număr de neclare triunghiular, care funcția de membru al formularului

.

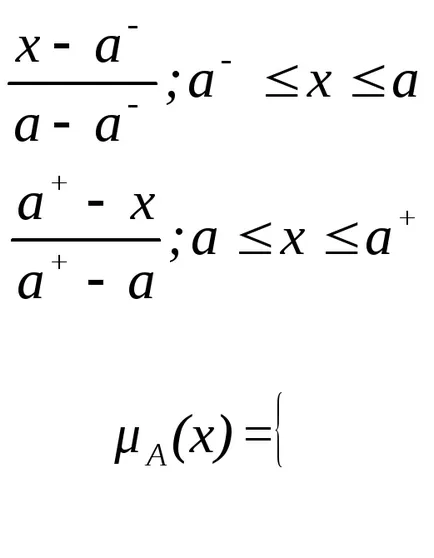
Mai mult decât atât, o proliferare a funcțiilor de membru în formă de trapez, care au forma

.

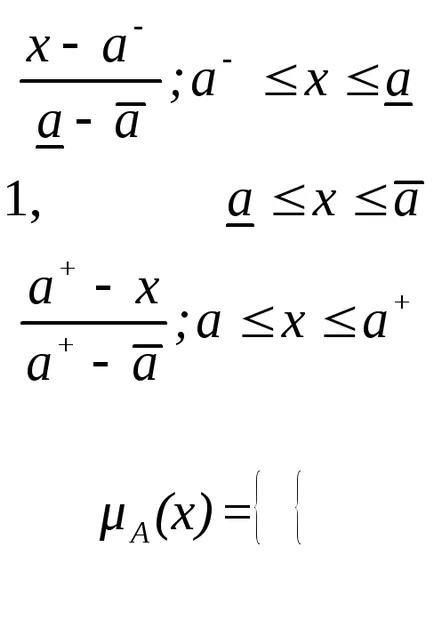
Solutia problemelor de modelare matematică a sistemelor complexe, utilizând seturile fuzzy necesită un volum mare de operațiuni pe diverse tipuri de variabile fuzzy, lingvistice și altele. Pentru comoditatea operațiunilor, precum și pentru IO și depozitare, este de dorit să opereze funcțiile de accesorii de tip standard.

Din păcate, chiar și cu reducerea numerelor fuzzy, la conceptul de numere triunghiulare, rămân o problemă nerezolvată a opus și a elementelor și proprietatea distributiv inversă. Un alt dezavantaj semnificativ al acestei abordări. Blur produs depinde nu numai de factorii încețoșare, dar, de asemenea, pe locul ocupat de date de numere fuzzy, pe axa reală. De exemplu, să

A = (1, 2, 3), B = (2, 3, 4), atunci AB = (2, 6, 12)

și C = (99, 100, 101), E = (100, 101, 102),

dacă CE = (9 900 10 100, 10 302).

Din acest exemplu rezultă că Consiliul Europei mai neclare decât AB.

Multimi fuzzy care trebuie să fie utilizate în cele mai multe sarcini sunt de obicei unimodale și normale. Una posibile metode de aproximare a mulțimilor fuzzy este aproximare unimodala folosind

- reprezentare.