Momentul de inerție, fizportal
moment de inerție
Pentru a calcula momentul de inerție, trebuie să împartă mental corpul în elemente suficient de mici, puncte care se poate considera că se află la aceeași distanță față de axa de rotație, apoi găsirea produsul masei fiecărui element cu pătratul distanței față de axa, și în final însumează tot produsul obținut. Evident, aceasta este o sarcină foarte consumatoare de timp. pentru a conta
momentele de inerție ale corpurilor de formă geometrică regulată, puteți utiliza într-un număr de cazuri, metodele de calcul integral.
Găsirea unei sume finită a momentelor de inerție ale elementelor corpului replace număr infinit însumarea mare de momente de inerție, calculate pentru elemente infinitezimale:
limi = 1 ∞ σδmi ri 2 = ∫r 2 dm. (La δm → 0).
Calculăm momentul de inerție al unui solid uniform disc sau înălțimea cilindrului h în raport cu axa sa de simetrie
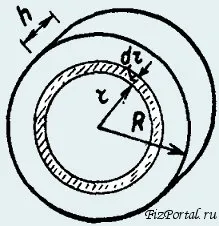
Dezmembreze unitate la elementele sub formă de inele concentrice subțiri centrate pe axa de simetrie. Inelul obținut are un interior și un diametru exterior r r + dr. și înălțimea h. Din moment ce dr <
i = σδmr 2 = r 2 σδm.
unde σδm - masa întregului inel.
Inel de deplasare 2πrhdr. Dacă densitatea materialului discului p. apoi masa inelelor
ρ2πrhdr.
Momentul de inerție al inelului
i = 2πρhr 3 dr.
Pentru a calcula momentul de inerție al întregului disc, este necesar să se rezuma momentele de inerție ale inelelor de centru (r = 0) până la marginea ei (r = R), adică se calculează integralei ..:
I = 2πρh 0 R ∫r 3 dr.
sau
I = (1/2) πρhR 4.
Dar masa discului m = ρπhR 2. în consecință,
I = (1/2) mR 2.
Să (fără a calcula) momentele de inerție pentru unele corpuri de formă geometrică regulată, realizate din materiale omogene
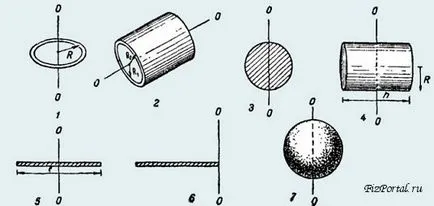
1. Momentul de inerție al unui inel subțire în jurul unei axe ce trece prin centrul său și perpendicular pe planul său (sau un cilindru tubular relativ subțire, cu pereți pe axa sa de simetrie):
I = mR 2.
2. Momentul de inerție al unui cilindru cu pereți groși în raport cu axa de simetrie:
I = (1/2) m (R1 2 - R2 2)
în care R1 - intern și R2 - raze exterioare.
3. Momentul de inerție față de axa de antrenare coincide cu una dintre diametrele sale:
I = (1/4) mR 2.
4. Momentul de inerție al unui cilindru solid în raport cu o axă perpendiculară pe generatoarea și extinzându-se prin mijlocul lui său:
I = m (R 2/4 + h 2/12)
unde R - raza bazei cilindrului, h - înălțimea cilindrului.
5. Momentul de inerție al unei tije subțiri în jurul unei axe care trece prin mijlocul ei:
I = (1/12) ml 2.
unde l - lungimea tijei.
6. Momentul de inerție al unei tije subțiri în jurul unei axe care se extinde printr-una dintre extremitățile sale:
I = (1/3) 2 ml
7. Momentul de inerție al bilă în raport cu o axă care coincide cu una dintre diametrele sale:
I = (2/5) mR 2.
În cazul în care un moment de inerție cunoscut al oricărui organism în raport cu o axă care trece prin centrul său de masă, moment de inerție în jurul oricărei axe paralele cu prima, pot fi găsite pe baza așa-numita teorema lui Huygens-Steiner.
Momentul de inerție în jurul oricărei axe I este momentul de inerție corp Ic în jurul unei axe paralele cu această trecere prin centrul de masă al corpului, plus m greutate. înmulțită cu pătratul l distanța dintre axele:
I = Ic + 2 ml.
Ca exemplu, vom calcula momentul de inerție al sferei de rază R și masa m. fire suspendate de o lungime l, în jurul unei axe care trece prin punctul O. Firul de suspensie în masă este mică în comparație cu masa balonului. Din momentul de inerție față de o axă care trece prin centrul de masă al Ic = (2/5) mR 2. o distanță
între axele (l + R), momentul de inerție față de o axă care trece prin punctul de suspensie:
I = (2/5) mR 2 + m (l + R) 2.
Dimensiunea momentului de inerție:
[I] = [m] x [r 2] = 2 ML.