Modalități de rezolvare a ecuațiilor algebrice
- ecuație polinomială de forma Pn (x) = 0, unde Pn (x) - n-th polinomul gradul ın raport cu x;
- ecuații raționale fracționare, adică, cuprinzând două componente ca privat două polinoame;
- ecuație irațional.
Pentru un număr de tehnici sunt o justificare teoretică. 30 prezintă tehnicile ilustrate mai mult de 36 de exemple. Nu cred că, având în exemplul specific, recepția este soluția cea mai rațională pentru acest exemplu. Trebuie doar să ia act de existența unei astfel de abordări pentru rezolvarea ecuațiilor.
Aceeași abordare (utilizarea trigonometrie, utilizarea de omogenitate, factoring etc.) sunt utilizate nu numai în relațiile cu rațional, de ecuații raționale, iraționale, dar, de asemenea, în soluția de ecuații, inegalități, sistemele transcendentale.
Aceste beneficii pot fi găsite număr suficient de ecuații necesare, desigur, fără a neglija alte surse.
1. Demonstrăm teorema: Dacă ecuația o x n + o -1x n -1 + ... + a1x + a0 = 0 (*) cu coeficienți întregi are o rădăcină rațională, unde p și q sunt relativ prime, atunci a0 divizibil cu p. și un împărțit la q.
Dovada: Înlocuim în (*) x pe. obține egalitatea numerică corectă, vom multiplica ambele fețe, cu q n:
Partea dreaptă este divizibil cu q. prin urmare, stânga trebuie să fie divizibilă cu q. ci pentru că p și q sunt relativ prim, atunci p n nu este divizibil cu q. dar atunci un trebuie să fie divizibilă cu q. în caz contrar partea stângă nu este divizibil cu q.
Partea dreaptă este un multiplu de p. De aceea, a lăsat un multiplu de p. dar q n sunt relativ prime la p. atunci a0 este un multiplu de p. Acest lucru dovedește teorema.
Dovada: Dividendul este egal cu împărțitorul înmulțit cu coeficientul plus restul. Deoarece divizorului - primul polinomul grad, iar restul va fi un polinom al cărui grad este mai mică decât cea a mijloacelor de divizare, reziduul - const. Câtul este un polinom de gradul n - 1. Apoi,
Când x = o ecuație are forma
din care rezultă P (a) = R. Teorema.
Consecință: Dacă x = a - radacina a polinomului, polinomul este împărțit de x - un nici un reziduu.
Dovada: Dacă ecuația x = a (***) devine 0 + R. = 0 ceea ce implică faptul că R = 0. Și din moment ce restul împărțirii este zero, atunci afirmația este demonstrată.
Exemplul 1. Rezolva ecuatia 30x 4 + x 3 - 30x 2 + 3x + 4 = 0.
Compoziția diferitelor fracții ireductibile ale căror numărătorii - divizorii termenului liber, adică, 4 și numitorii - divizori conducere coeficient, adică 30.
În coloana din stânga la numitor include toate divizori de 30. Este evident că - 1 - rădăcina polinomului. Prin corolar al teoremei Bézout divide polinomul la x + 1
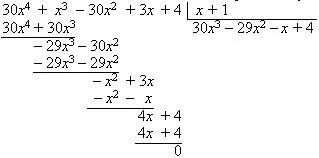
Pentru a găsi rădăcinile polinomului 3 30x - 29x 2 - x + 4 utilizarea fracțiunilor de masă. Când polinomul ia forma aceea, - rădăcina polinomului.
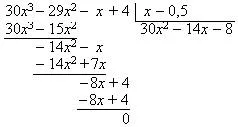
2. În rezolvarea ecuațiilor algebrice pot fi metoda utila coeficienților nedeterminat.
Exemplul 2: rezolva ecuația x 4 + 2x 3 - 16x 2 + 11x - 2 = 0.
Să polinomul reprezentat ca produsul
în cazul în care un. b. g. a. b. Coeficienții c, care sunt de dorit să fie selectate astfel încât după paranteze expansiune și reducând termenii similari transformat polinom original. Eliminăm paranteze, presupunând că a = a = 1.
Să c = 1, g = - 2 sau c = 2, g = - 1 (selectați coeficienți).
b = - 3, b = 5 atunci.
Pretindem că b = 5, g = - 2, b = - 3, c = 1. Acest set satisface toate cele patru ecuații, deci putem scrie
Având ecuații pătratice rezolvate, vom găsi rădăcinile ecuației originale.
3. Decizia de ecuații recurente
După termenul prin termenul împărțit la x k. acestea sunt rezolvate prin substituirea
Exemplul 3. 4 Rezolvarea ecuației 2x - 3x 3 - 7x 2 -15x + 50 = 0.
Divide prin x 2. obține
Ecuația devine:
Dacă l = 1, atunci ecuația de forma ax + 2k 2k -1 bx + cx + dx -2 2k 2k + -3 ... + dx 3 + cx 2 + bx + a = 0 se numește întoarcere (sau simetrică) prin ecuația primului tip de grad 2k .
Exemplul 4. Rezolvați ecuația 4 + 3x 5x 3 - 16x 2 + 3x + 5 = 0.
Noi împărțim termenul de termenul de x 2. Avem.
Dacă l = - 1, obținem ecuația formei
ax + 2k 2k -1 bx + cx + dx -2 2k 2k + -3 ... + dx 3 + cx 2 - bx + a = 0, ceea ce se numește o întoarcere (sau simetrică) ecuație gradul 2k al doilea tip. Acesta este rezolvată prin substituirea
Exemplul 5 Rezolva ecuația 8x 4 - 42x 3 + 29x 2 + 42x + 8 = 0.
polinom palindrom de grad impar are o rădăcină - 1. Acest lucru se datorează faptului că ecuația are un număr par de membri, atunci când înlocuiți x prin - 1 perechi sunt distruse. Prin urmare, la începutul polinomului este împărțit la x + 1, iar coeficientul va duce la ecuația revenirea chiar grad, o decizie care a fost deja discutată.
Exemplul 6. Rezolva ecuația 5 24x + 74x 4 - 123x 3 - 123x 2 + 74x + 24 = 0.
Avem gradul 5-polinomială palindrom. Una dintre rădăcinile sale - 1. Prin împărțirea la x + 1, obținem
Potrivit lui Newton binomu
Nota 2. Se determină aspectul că ecuația este revenirea nu este întotdeauna ușor, mai ales dacă. Prin urmare, în ecuația de gradul 2n producem termwise diviziunea x n și în cazul în care acest lucru dă o sumă de expresii. unde n = 0, 1, 2 ... m. apoi o altă decizie este clar.