Metoda grafică pentru rezolvarea ecuațiilor în Microsoft Excel 2018 mediu

Tipul lecției: Sinteza, consolidarea materialului și explicarea noilor.

Scopurile și obiectivele lecției:

Echipamente, calculatoare personale, proiector multimedia, ecran de proiecție.

Materiale pentru lecție: prezentarea Power Point pe calculatorul profesorului (a se vedea anexa 1).

Slide 1 din Prilozheniya1 (link-urile către slide-urile merg fără Prilozheniya1).

1. Activitatea orală (actualizarea cunoștințelor).

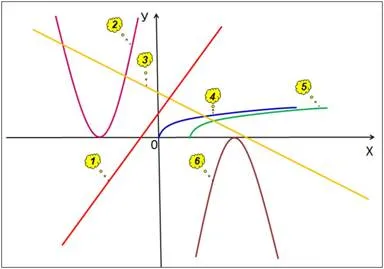
Slide 2 - Corespondențe următoarele funcții cu diagramele din desen (Figura 1.):

y = 6 - x; 2x + y = 3; y = (x + 3) 2; y = - (x - 4) 2; .

Slide 3 soluții grăitor de ecuații de forma (x) = 0 f.

Rădăcinile ecuației f (x) = 0 sunt valorile x1. X2, ... a generat puncte de trecere ale y = f (x), cu axa orizontală (fig. 2).

Găsiți rădăcinile ecuației x 2 -2x-3 = 0. folosind o metodă grafică de rezolvare a ecuațiilor (Figura 3).

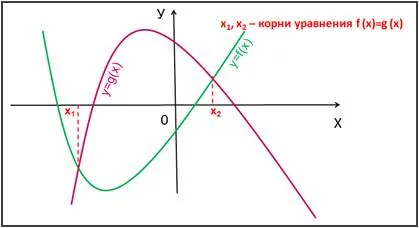
Slide 5 soluții Metoda grafică de ecuații de forma f (x) = g (x).

Rădăcinile ecuației f (x) = g (x) sunt valorile x1. x2, ... punctelor de intersecție ale funcției grafice y = f (x) și y = g (x). (Figura 4.):

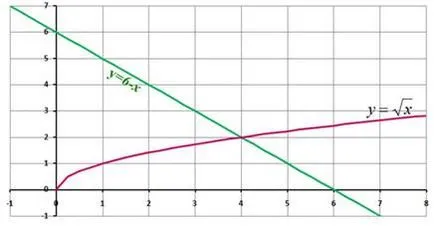
Slide 6 Găsiți rădăcinile ecuației, folosind o metodă grafică de rezolvare a ecuațiilor (Fig. 5).

2. O explicație a noului material. Lucrări practice.

mod I.Grafichesky de a rezolva ecuațiile de forma f (x) = 0 în Excel.

Mai multe de lucru ca profesor în Excel în același timp cu studenții, cu detaliate (dacă este necesar) instrucțiuni și afișează rezultatele pe un ecran de proiecție. Lamelele Apendicele 1 sunt utilizate pentru formularea obiectivelor și totalizarea subtotaluri.

Exemplul 1: Utilizarea diagramelor în Excel, metoda grafică pentru a rezolva ecuația 2 -x + 5x-4 = 0.

Pentru a face acest complot functia y = -x 2 + 5x-4 în intervalul [0; 5], cu creșteri de 0,25; \ Găsiți valoarea x a graficului punctelor de intersecție cu axa x.

O sarcină poate fi împărțit în etape:

Etapa 1: Introducerea funcțiilor în formă de tabel (Figura 6) .:

• în celula A1 introduceți textul în H. ​​celula A2 - Y;
• în celula B1 introduceți numărul 0, celula C1 - numărul de 0,25;
• evidențiați celulele B1: C1. muta cursorul mouse-ului pentru a evidenția un marker, iar în momentul în care se schimbă indicatorul mouse-o cruce neagră, pentru a ajunge la mânerul de selecție dreapta la V1 celulei (fig. 7).

După intrarea în celula ar avea ca rezultat formula de calcul cu formula și formule în câmpul șir de intrare - formula în sine (Figura 8.):

• copiați conținutul celulelor B2 în celula C2: V2 pentru markerul de selecție. Intreaga gama de celule selectate umplute cu conținutul primei celule. În această celulă trimiterile din formulele schimbă în raport cu prejudecată formula însăși.

Etapa 2: construcția diagramelor de tip grafic.

• selectați intervalul de celule B2: V2;
• Fila Insert | Chart | Chart alege tipul de program;
• (. Figura 9) | pe fila Proiectare Selectați datele din fereastra „sursă de date Selectare“ click pe butonul Edit din Semnături axei orizontale - deschide o fereastră „Semnăturile axei.“ Aloca o serie de celule din tabelul B1: V1 (valoarea variabilei x). În ambele ferestre, făcând clic pe OK;

• pe fila Aspect | Axe | Rezumat axa orizontală | Parametrii suplimentari ai axa orizontală principal pentru a selecta:

Intervalul dintre marcajele 4;

Intervalul dintre semnăturile: Interval de unitate: 4;

Axa Regulamentul de diviziuni;

Selectați lățimea și culoarea liniei (filele tip de linie și culoarea liniei);

• schimba independent lățimea și culoarea liniei pentru axa verticală;
• pe fila Aspect | Grila | verticale liniile de grilă axa principală pentru a alege liniile principale de rețea.

Un rezultat operație exemplar este prezentat în Fig. 10:

Etapa 3: Se determină rădăcinile ecuației.

Graful y = -x 2 + 5x-4 intersectează axa x la două puncte și, prin urmare, ecuația 2 -x + 5x 4 = 0 are două rădăcini: x1 = 1; x2 = 4.

II. Metoda grafică de rezolvare a ecuațiilor de forma f (x) = g (x) în Excel.

Exemplul 2: rezolva ecuația grafic.

Pentru a face acest lucru într-un singur sistem pentru a parcelei funcții de coordonate și y1 = y2 = 1-x în intervalul [-1; 4], cu creșteri de 0,25; găsi valoarea lui x este punctul de intersecție a graficelor de funcții.

Etapa 1: Introducerea funcțiilor în formă de tabel (Figura 1.)

• Du-te la Foaie2.
• Ca și în exemplul 1. Când copiați tehnici, completați în tabel. Când tabulating funcția y1 = utilizați încorporat rădăcină (Fig. 11).

Etapa 2: construcția diagramelor de tip grafic.

Un rezultat operație exemplar este prezentat în Fig. 12:

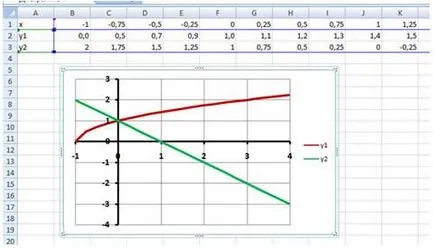
Etapa 3: Se determină rădăcinile ecuației.

Grafice funcțiilor și y1 y2 = 1-x = se intersectează într-un punct (0, 1) și, prin urmare, ecuația are o radacina - abscisa punctului x = 0.

III.Metod caută.

Metoda grafică de ecuații de rezolvare este frumos, dar nu întotdeauna punctul de intersecție poate fi la fel de „bun“, în exemplele special selectate 1 și 2.

Oportunități foi de calcul vă permit să localizați valorile aproximative ale cailor ecuației cu o anumită precizie. Pentru a face acest lucru, utilizați parametrul de selectare a metodei.

Exemplul 3. Să considerăm o metodă de selecție a parametrului de exemplu soluțiile ecuației 2 -x + 5x-3 = 0.

Etapa 1: construcția diagramelor de tip grafic pentru determinarea aproximativă a rădăcinilor ecuației.

Se trasează functia y = -x 2 + 5x-3. editare a obținut în exemplul 1 formulă.

• dublu-clic pe celula B2. a face modificările necesare;
• folosind marker de selecție copie formula în toate celulele pe C2: V2.

Toate modificările sunt afișate imediat pe grafic.

Un rezultat operație exemplar este prezentat în Fig. 13:

Etapa 2: Determinarea valorilor aproximative ale rădăcinilor ecuației.

Graful y = -x 2 + 5x-3 intersectează axa orizontală în două puncte și, prin urmare, ecuația 2 -x + 5x 4 = 0 are două rădăcini.

Conform programului, putem determina cu aproximație, care x1 ≈0,7; x2 ≈4,3.

Pasul 3: Găsiți o soluție aproximativă la o anumită precizie de Goal Seek.

1) Începeți cu căutarea de valoare mai precisă rădăcină mai mici.

Din grafic este evident că argumentul la cel mai apropiat punct de intersecție al graficului cu axa orizontală este de 0,75. Valorile din tabel funcție, acest argument este plasat în E1 celula.

• Selectați E2 celulă;
• du-te la tab-ul de date | Analiza „what-if» | Goal Seek ...;

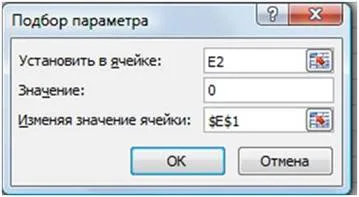
În dialog parametrul de selecție box (. Figura 14) în câmpul Value pentru a introduce valoarea dorită a funcției: 0.

În valoarea schimbare a celulei. introduceți $ E $ 1 alineatul (click pe celula E1).

Faceți clic pe butonul OK.

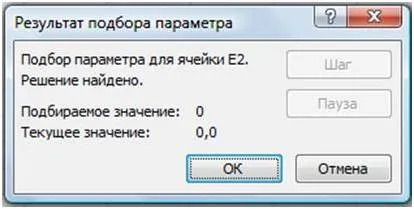
• (. Figura 15) În rezultatul selecției afișează informații despre valoarea selectată și corespund valorilor:
• Celula E1 ieșire ales 0.6972 valoare argument cu o precizie dorit (0,0001).

Set de precizie se poate realiza prin instalarea în celulele de tabel reprezentarea exactă a numerelor - numărul de zecimale (Format Cells | Număr | Numeric).

Deci, prima rădăcină a ecuației este definită cu o anumită precizie: x1 ≈0,6972.

2) găsi propria lor valoare mai mare rădăcină cu aceeași precizie. (X2 ≈4,3029).

Parametrul selecție IV.Metod pentru soluțiile de ecuații de forma f (x) = g (x).

Când se folosește metoda pentru a selecta parametrii pentru soluția ecuațiilor de forma f (x) = g (x) este introdusă o funcție y auxiliară (x) = f (x) -g (x) și găsiți precizia cerută valoarea x a graficului punctele de intersecție y (x) abscisa.

3. Fixarea materialului studiat. Munca independentă.

Sarcina: Utilizarea metodei de selectare a parametrilor pentru a găsi rădăcinile de până la 0,001.

• introduceți funcția y = și se construiește graficul acesteia pe intervalul [-1; 4], cu creșteri de 0,25 (fig.16.):

• găsi o valoare aproximativă x graficului punctelor de intersecție cu abscisa (x ≈1,4);
• găsi o soluție aproximativă de până la 0,001 de parametrul de selecție (x ≈1,438).

4. Rezultatul lecției.

Slide 12 Rezultatele testelor de lucru independente.

Slide 13 Repetând procesul de soluțiile grafice ale ecuației f (x) = 0.

Slide 14 Repetând procesul de soluțiile grafice ale ecuației f (x) = g (x).

5. Tema.

Utilizarea în Excel și diagrame parametru de selectare a metodei, determină rădăcinile -5H x 2 + 2 = 0 până la 0,01.