Mathcad construi o cutie si un poligon arbitrar în 3d

MathCad: a construi o casetă și poligoane arbitrare în 3D

De fapt, cub tridimensional în MathCad poate fi reprezentat de un poliedru „funcție secretă“ ( „# 11“) (pentru mai multe detalii în acest articol al meu). Dar ce se întâmplă dacă nu nevoie doar de un cub și o cutie sau, de exemplu, axa X. Y. Z nu doresc să-și petreacă în cazul în care deține MathCad - în colțul de 3D-câmp, și locul lor de drept la origine?

Standard înseamnă într-un fel nu se produce, dar dacă o plimbare distracție cu contextul vector matkadovskim, atunci puteți face aproape orice. Cum ar fi spune VF Puncte. Derivare. există, de asemenea, de divertisment și de ajutor.

În această notă avem deja codul pentru a construi punctul sau segmentul în graficele tridimensionale. În acest caz, a segmentelor pot fi compuse din orice cadru, inclusiv, și cutia. Pentru simplificare, vom face partea lui paralelă cu axele, iar paralelipipedul cere două noduri diagonal opuse ale P și Q.

Mathcad axa petrecut vizibil prin origine, definim Ox funcția auxiliară. Oy. Oz (pe diagramă - linia albastră). Dimensiunea axelor depinde de valoarea unui. arătând limitele regiunii care urmează să fie afișate sunt aceleași în toate cele trei dimensiuni. Asta e tot calcul:

O cutie de dreapta și axe în Mathcad

După cum se poate observa, nu este necesară funcția metodei Piped Point, este suficient pentru a transmite coordonatele doi vectori de coloane ale fiecărui element 3, prezentând coordonatele nodurilor opuse ale paralelipipedului.

În ceea ce privește linia întreruptă, aceasta poate fi o linie rupt de segmente, și este posibil și simplu de a construi un arbitrar nodurile poligon din N scrise în vectorul 3 rând (dimensiunea elementelor N) x secvență, y și z-coordonatele de noduri și apoi scrie-l în vectorul coloană. Ambele metode prezintă un exemplu, și, în ambele cazuri, linia zamknom rupt făcând coordonatele ultimului punct coincide cu primele coordonate.

Mathcad: construirea de inclinare spațiu tridimensional

A doua opțiune este în mod clar de preferat, deoarece nu necesită duplicarea datelor, solicită funcția suplimentară Punct. și, în plus, este construirea unui singur obiect în loc de N obiecte diferite. Prin urmare, toate ușor de spart vopsi sau înlocuiți-l grosime.

In concluzie, vom construi un tetraedru regulat cu vârfuri A la originea și vârf B la (1,0,0). În acest moment C, de asemenea, situată în coordonatele planul XY va fi (1/2 rădăcină (3) / 2, 0). și "superior" vertex S - coordonatele (1/2 rădăcină (3) / 6, radacina (6) / 3).

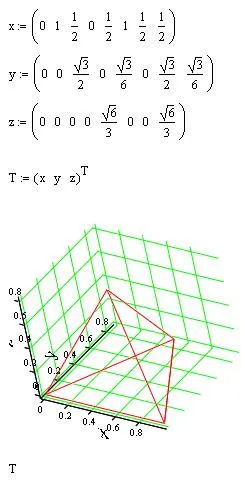
Mathcad: cum de a construi un tetraedru regulat cu coordonatele nodurilor date

Coordonatele primului punct nu coincide cu coordonatele ultimei, dar cifra este închis. Doar una dintre margini este deplasată de două ori, și anume, suntem pe marginile „traseu“ AB - BC - CA - AS - SB - BC - CS. În jurul toate marginile tetraedrul, având doar o singură dată, este imposibil pentru fiecare margine.