matematici superioare
Să o anumită valoare în schimbare y. în funcție de variabila x. Presupunem că această variabila x poate fi modificată astfel încât să îndeplinească o condiție B >>. „abordări“ variabile ( „angajate“) la ceva (ceea ce înseamnă că vom actualiza mai târziu, cu ajutorul unor definiții stricte). Apoi, se pune întrebarea, nu se efectuează în cazul în care y este orice mod „corect“, de asemenea, „încercând“ ceva, de exemplu, la numărul de L. Dacă este așa, acest „ceva“ se numește limita de y pentru o anumită condiție B >> pentru x și se notează
Dăm acum o definiție strictă a limitei, în unele cazuri speciale, și apoi se trece la o discuție a definiției generale.
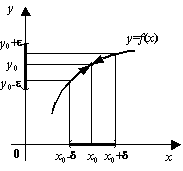
Să y = f (x) - este o funcție a variabilei x reală. definit în toate punctele intervalului (a, b). cu excepția, eventual, la punctul x 0 ∈ (a, b) \ (a; b)>. Să ne definim valoarea limită a y, cu condiția ca x se apropie de punctul x 0>. Această condiție este indicată printr-o scurtă x → x 0>. Dorința x la x 0> înseamnă că, atunci când schimbați x sa apare într-o tot mai îngustă în vecinătatea din jurul punctului x 0>. dar nu identică cu x 0>. adică, valoarea | x - x 0 | \ Vert> devine din ce în ce mai mici, mai aproape de 0, dar nu devine zero. Se poate întâmpla ca x valoarea y = f corespunzătoare (x) se apropie și mai aproape de un număr fix y 0>. Mai mult decât atât, pentru orice cartier arbitrar mic de y 0>, puteți specifica cât de strâns x trebuie să vină la x 0>. valorile y = f (x) au apărut deja în vecinătatea y 0>. Apoi, numărul y 0> este limita funcției f (x), cu condiția ca x → x 0>. care este scris după cum urmează:
Formaliza a spus pentru a da o mai mare claritate matematică. Orice vecinătate a punctului y 0> (simetrică în raport cu y 0>) se caracterizează prin sale semiamplitudine e> 0> 0>. adică are intervalul formă (y 0 - ε; y 0 + ε) -; y _ +)>. În cazul în care valoarea lui y sunt într-o astfel de e> este un cartier, aceasta înseamnă că | y - y 0 | <ε \vert <> . Fiecare cartier din x 0>. care nu conține mai punctul x 0> (și simetric în raport cu x 0>), - o asociație a două intervalov3 adiacente (x 0 - δ; x 0) ∪ (x 0, x 0 + δ) = (x 0 - δ; x 0 + δ) ╲
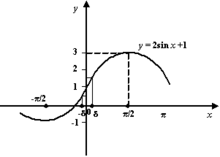
Pentru a face acest lucru, vom repara un număr arbitrar de e> 0> 0>. specificând o vecinătate a lui (1 - ε; 1 + ε); 1 +)>. și de a determina la ce valori de x f (x) va scădea în vecinătatea 1.
Să luăm acum în considerare o altă limită caz important.
Din această ecuație (1) rezultă că odată cu creșterea în număr de n termeni pozitivi în creșterile în partea dreaptă. Mai mult, prin creșterea numărului n n >> 1 scade, astfel încât valoarea (1 - 1 n). . (1 - 2 n)> \ dreapta), \ la stânga (1 -.> \ Dreapta)> crește. Prin urmare, secvența
Arătăm că este limitată. Înlocuiți fiecare suport de pe partea dreaptă de către unul, partea dreapta va crește, obținem inegalitatea
Consolidarea inegalitatea rezultată, înlocuiți 3,4,5, ... stând la numitorul numărului fracției 2:
Cantitatea de suportul conform formulei vom găsi suma dintre membrii progresie geometrică:
Astfel, secvența este mărginită de mai sus, în care 8 n 2 N> n>
\ Mathbb> inegalitățile (2) și (3) 2 <( 1 + 1 n ) n <3
Prin urmare, în baza teorema Weierstrass (secvență criteriu de convergență), secvența x n = (1 + 1 n) n. n 2 N = \ stânga (1 +> \ dreapta) ^, n>
\ Mathbb> în creștere și mărginită monoton, atunci limita este reprezentat de litera e. Ie lim n → ∞ (1 + 1 n) n = e \ stânga (1 +> \ dreapta) ^ = e >>>
Știind că a doua limită remarcabilă pentru adevăratele valori x pozitive, se dovedesc a doua limita remarcabila reale x, adică dovedesc că lim x → ∞ (1 + 1 x) x = e; x 2 R \ left (1 +> \ dreapta) ^ = e; x>
\ Mathbb>. Considerăm două cazuri:
1. Fie x → + 1 >>. Fiecare valoare a lui x se află între două numere naturale: n ⩽ x
Din aceste două cazuri, implică faptul că lim x → ∞ (1 + 1 x) x = e \ stânga (1 +> \ dreapta) ^ = e> real x.
O proprietate interesantă a doua limită remarcabil este că arată un interes depozit bancar la capitalizarea nepriryvnoy. Să presupunem că contribuția procentuală p. Apoi, pentru valorificarea ori pe an, obținem S * (1 + p). Atunci când capitalizarea o dată pe lună obținem: S * (1 + p / 12) 12>. Când nepriryvnoy kapitazizatsii obține: S * lim x → ∞ (1 + p x) x = S * e p \ left (1 +> \ dreapta) ^ = S * e ^>
lim x → ∞ x (ln (x + 1) - ln (x)) = lim x → ∞ x (ln x + 1, x) = lim x → ∞ x (ln (1 + 1 x)) = lim x → ∞ ln (1 + 1 x) x = ln e = 1 x \ stânga (\ ln (x + 1) - \ ln (x) \ dreapta) = \ lim _x \ stânga (\ ln> \ dreapta) = \ lim _x \ stânga (\ ln (1 +>) \ dreapta) = \ lim _ \ ln (1 +>) ^ = \ ln e = 1> == Tabelul infinitezimal echivalent la x → 0 = = e7x / tg3x