Lungimea arcului eliptic
b - axa minoră;
x 2 / a 2 + y 2 / b 2 = 1 - ecuația canonică a elipsei;
t1 - stabilirea primului punct al arcului;
t2 - stabilirea al doilea punct al arcului;
t - variabila parametric - unghiul dintre axa ordonatelor și punctul raza vectorului elipsă;
x = Asint - abscisa ecuația parametrică a elipsei;
y = bcost - coordona ecuația parametrică a elipsei;
Ldug.ell - lungimea arcului eliptice.
[Regula] Formula
[Math] L _> = Ae \ stânga (\ varepsilon, t_2 \ dreapta) -ae \ stânga (\ varepsilon, t_1 \ dreapta), \ \ varepsilon = \ frac> \ 0 \ le t_1 \ le t_2 \ le \ frac \ Leftrightarrow [/ matematica] [matematica] \ Leftrightarrow L _> = Ae \ stânga (\ frac>, t_2 \ dreapta) -ae \ stânga (\ frac>, t_1 \ dreapta), \ 0 \ le t_1 \ le t_2 \ le \ frac [/ math]- Perimetrul elipsei este egal cu Pell = 4AE (ε, tt / 2).
[Regula] formula Concluzie
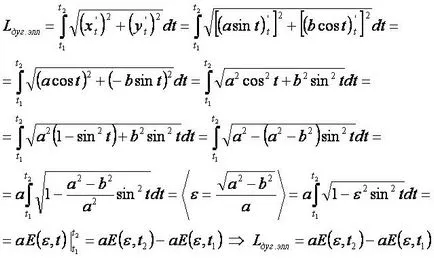
- Pentru a obține formula de „lungimea arcului curbei plane“ este utilizat în formă parametrică (parametrul t - este unghiul dintre axa ordonatelor și punctul elipsa vector raza).
- Pentru a găsi integralei utilizează eliptică tip integral II.