Liniare omogene ecuații diferențiale a doua ordine cu coeficienți constanți,

In acest articol, vom examina principiile soluției de ecuații liniare diferențiale a doua ordine omogene cu coeficienți constanți, în care p și q - sunt numere reale arbitrare. Prima oprire pe teoria, apoi se aplică rezultatele în rezolvarea de exemple și probleme.

Dacă veți întâlni termeni nefamiliare care se referă la definițiile și conceptele teoriei ecuațiilor diferențiale.

Să ne formulăm o teorema care specifică forma în care pentru a găsi o soluție comună de ecuații liniare diferențiale ordinare.

Soluția generală a unei ecuații diferențiale omogene liniare cu continua pe intervalul de integrare este determinat de coeficienți de combinare X liniare, în care - soluții particulare liniar independente pentru liniare Ecuații ordinare diferențiale și X. - constante arbitrare.

Astfel, soluția generală a unei ecuații diferențiale omogene a doua ordine liniară, cu coeficienți constanți de forma y0 = C1 ⋅y1 + C2 ⋅y2. unde și y1 y2 - soluții particulare liniar independente, și C1 și C2 - constante arbitrare. Rămâne să învețe cum să găsească soluții special Y1 și Y2.

Euler a propus să caute soluții speciale în formă.

Dacă luăm o soluție specială de ecuatii diferentiale liniare ordinare de ordinul al doilea, cu coeficienți constanți, ecuația trebuie pentru a obține identitatea prin substituirea acestei soluții:

Deci avem așa-numita ecuație caracteristică unei liniare omogene de ordinul a doua ecuații diferențiale cu coeficienți constanți. Soluții și k1 k2 ecuației caracteristice determină particulare soluțiile și ecuațiile diferențiale liniare ale ordinul doi cu coeficienți constanți.

În funcție de coeficienții de p și q sunt rădăcinile ecuației caracteristice pot fi:

1. reale și diferite,
2. valabile și de potrivire,
3. pereche complex conjugat.

În primul caz, soluțiile particulare sunt liniar independente ale ecuației diferențiale inițiale și sunt soluții generale liniare ecuațiilor diferențiale ordinare de ordinul doi cu coeficienți constanți sunt.

Funcții și într-adevăr liniar independente, deoarece Wronskian nu este zero pentru orice x real.

În al doilea caz, o anumită soluție este o funcție. Într-o a doua soluție particulară este luată. Vom arăta că într-adevăr, o soluție specială de liniare Ecuatii diferentiale ordinare de ordinul al doilea, cu coeficienți constanți și să dovedească independența liniară a Y1 și Y2.

Deoarece k1 = k0 și k2 = k0 coincidente rădăcinile ecuației caracteristice, atunci aceasta are forma. În consecință, - ecuația diferențială liniară omogenă inițială. Membru supleant în ea și asigurați-vă că ecuația devine o identitate:

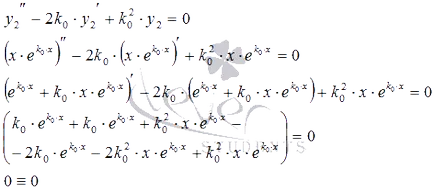
Astfel, o soluție particulară a ecuației inițiale.

Arătăm independența liniară a funcțiilor și. Pentru a face acest lucru, vom calcula Wronskian și asigurați-vă că acesta este diferit de zero.

Concluzie: liniar independente soluții particulare ale ecuațiilor diferențiale liniare ordinare ale ordinul doi cu coeficienți constanți sunt și, iar soluția generală este la.

În al treilea caz, avem un cuplu de soluții complexe și parțiale de ecuații liniare diferențiale ordinare. Soluția generală este scrisă. Aceste soluții speciale pot fi înlocuite cu două funcții reale și părțile reale și imaginare corespunzătoare. Se poate observa în mod clar, în cazul în care convertiți o soluție comună, folosind formule din teoria funcțiilor unui tip de variabilă complexă:

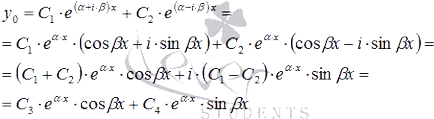
unde C3 și C4 - constante arbitrare.

Așa că am generaliza teoria.

Algoritmul de găsire a unei soluții generale a unei ecuații omogene liniare diferențiale de ordinul doi cu coeficienți constanți.

1. Scriem ecuația caracteristică 2 k + p ⋅ k + q = 0.
2. Noi găsim rădăcinile ecuației caracteristice și k1 k2.
3. În funcție de valorile rădăcinilor ecuației caracteristice este soluția generală a ecuațiilor diferențiale ordinare liniare cu coeficienți constanți în formă de:
   • , în cazul în care;
   • , în cazul în care;
   • , în cazul în care.

Luați în considerare exemplele în fiecare caz.

Găsiți soluția generală a unei omogene de ordinul a doua ecuații diferențiale liniare cu coeficienți constanți.